Векторы. Линейное векторное пространство

Аналитическая геометрия

Вектор - это направленный отрезок с начальной и конечной точкой. Его можно перемещать параллельно самому себе.

На рисунке 7.1 представлен вектор АВ с начальной точкой А и конечной точкой В.

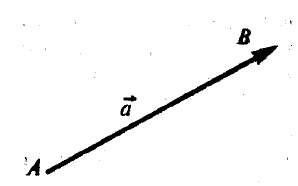
Рисунок 7.1 - Вектор

Длина (модуль, норма) вектора – длина отрезка, изображающего вектор.

Произведением вектора 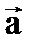на число l называют вектор 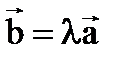, длина которого 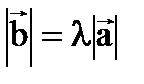, а направление совпадает с направлением вектора 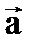, если l > 0, и противоположно ему, если l < 0.

Противоположный вектор - это произведение вектора на число (-1) (т.е. длина противоположного вектора такая же, а направление - противоположное).

Коллинеарные векторы - это векторы, лежащие на одной прямой или на параллельных прямых. Вектора коллинеарны тогда и только тогда, когда один из них равен произведению другого на некоторое число (в самом деле, направления таких векторов либо совпадают, либо противоположны, и они отличаются только длиной).

Нулевой вектор – это вектор, у которого начало и конец совпадают. Его длина равна нулю. Принято считать, что он коллинеарен любому вектору.

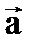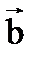Суммой двух векторов и называют вектор 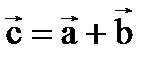, начало которого совпадает с началом вектора 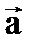, а конец - с концом вектора 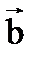при условии, что начало вектора 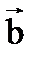совпадает с концом вектора 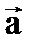.Такое определение суммы получило название правила треугольников (см. рисунок 7.2).

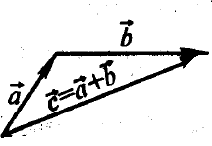
Рисунок 7.2 – Понятие суммы векторов

Поскольку любой вектор можно переносить параллельно самому себе, это определение дает возможность найти сумму любых векторов. Кроме того, понятие суммы векторов можно обобщить на любое число векторов (см. рисунок 7.3).

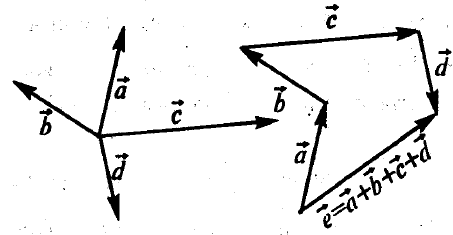
Рисунок 7.3 – Сумма четырех векторов

Координаты вектора представляют собой разность между координатами его конца и начала; т.е. если вектор имеет начало А = (x₁, y₁) и конец B = (x₂, y₂), то его координаты = (x₂ – x₁, y₂ - y₁). Если перенести вектор 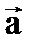так, чтобы его начало совпало с началом координат, т.е. с точкой
О = (0, 0), то координатами вектора будут координаты его конечной точки.

Координаты вектора в n-мерном пространстве определяются точно так же. Поэтому можно дать другое определение понятия вектора: n-мерный вектор- это упорядоченная совокупность n действительных чисел, записываемых в виде Х = (х₁, х₂,...,х_n), где x_i - i-я компонента вектора X.

При этом можно считать, что каждая из этих координат является разностью между соответствующими координатами конца и начала вектора (только увидеть этот «направленный отрезок» в пространстве более высокой размерности, чем трехмерное, невозможно, т.к. оно представляет собой научную абстракцию).

Можно доказать, что сумму векторов X = (х₁, х₂,...,х_n) и
Y = (y₁, y₂,...,y_n) любой одинаковой размерности можно рассчитать по формуле:Z = X + Y = (х₁ + y₁, х₂ + y₂,..., х_n + y_n); а произведение вектора X на число l - по формуле lX = (lх₁, lх₂,..., lх_n). Иными словами, эти операции определяются так же, как сложение или умножение на число матрицы-строки (или матрицы-столбца).

Рассмотренные операции над векторами обладают следующими свойствами, которые вводятся аксиоматически:

1) Коммутативный (переместительный) закон сложения:
X + Y = Y + X.

2) Ассоциативный (сочетательный) закон сложения:
(X + Y) + Z = X + (Y + Z).

3) Ассоциативный (сочетательный) закон относительно числового множителя: .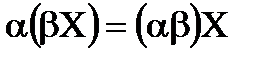

4) Дистрибутивный (распределительный) закон умножения относительно суммы векторов: .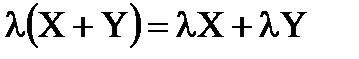

5) Дистрибутивный (распределительный) закон относительно суммы числовых множителей: .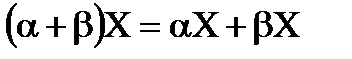

6) Особая роль нулевого вектора для суммы: X + 0 = A.

7) Наличие противоположного вектора -X такого, что X + (-X) = 0.

8) Нейтральность единицы при умножении: 1*X = X.

Множество векторов, в котором определены операции сложения векторов и умножения вектора на число, обладающие вышеприведенными свойствами, называют линейным векторным пространством.