Метод Ньютона (метод касательных).

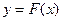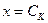Его отличие от предыдущего метода состоит в том, что на К-ой итерации вместо хорды проводится касательная к кривой при , и находится в точках пересечения касательной с осью абсцисс. При этом не обязательно задавать [а,b], содержащий корень. Достаточно лишь найти некоторое начальное приближение корня 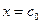(рисунок 12. 2).

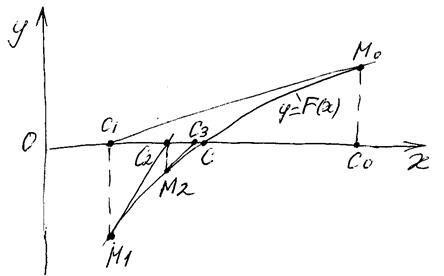
Рисунок 12. 2 Метод Ньютона.

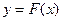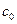Уравнение касательной, проведенной к кривой в точке с координатами и 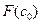, имеет вид:

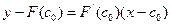. (12.3)

Отсюда находим следующее приближение корня 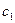, как абсциссу точки пересечения касательной с осью .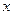

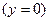. (12.4)

Аналогично могут быть найдены и следующие приближения 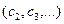как точки пересечения с осью абсцисс касательных, проведенных в точках 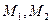и т.д. Формула для 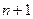приближения имеет вид:

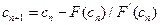. (12.5)

При этом необходимо, чтобы 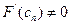. Для окончания итерационного процесса может быть использовано условие 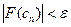, или условие близости двух последовательных приближений:

.

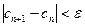В этом методе объем вычислений в каждой итерации больше, т.к. надо вычислять производную функции, но скорость сходимости значительно возрастает по сравнению с другими методами.