Блок-схема метода Гаусса-Зейделя.

В качестве исходных данных вводятся коэффициенты и правые части уравнений системы, погрешность ε, допустимое число итераций М, а также начальные приближения переменных 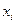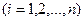, как показано на рис. 10.1. Начальные приближения можно не вводить в программу, а полагать их равными некоторым значениям, например нулю.

Обозначения: К - порядковый номер итерации; 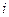- номер уравнения; а также переменного, которое вычисляется в данном цикле; 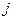- номер члена вида 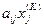в правой части соотношения (10.9):

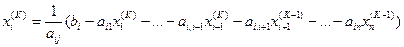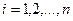, . (10.9)

δ – критерий окончания итерационного процесса.

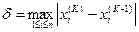< ε. (10.10)

Итерации прекращаются либо после выполнения условия (10.10), либо при К=М.

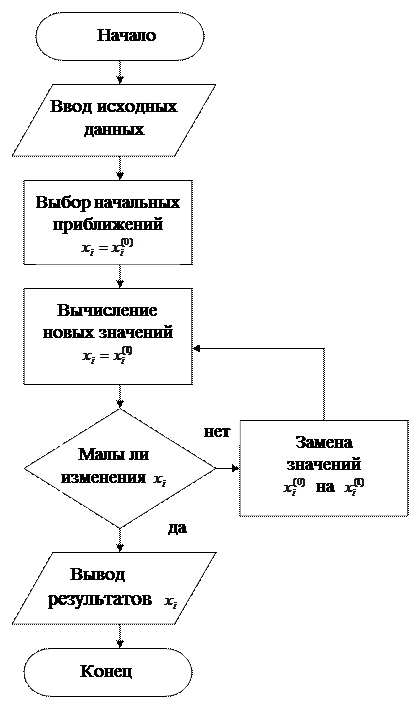
Рисунок 10.1 Блок-схема решения систем уравнений методом итераций.