Метод Гаусса-Зейделя.

Этот метод является одним из самых распространенных итерационных методов, отличается простотой и легкостью программирования.

Рассмотрим этот метод на примере решения системы трех уравнений:

,

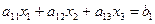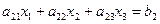, (10.1)

.

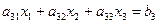Предположим, что диагональные элементы 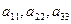отличны от нуля. Выразим неизвестные соответственно из 1,2,3 уравнений системы:

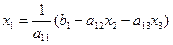, (10.2)

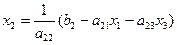, (10.3)

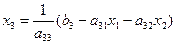. (10.4)

Зададим некоторые начальные (нулевые) приближения значений неизвестных:

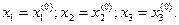
Подставляя эти значения в правую часть выражения (10.2) получаем новое (первое) приближение для :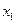

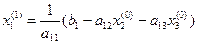. (10.5)

Используя это приближение для 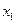и приближение 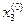для 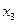, находим из (10.3) первое приближение для :

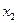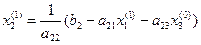. (10.6)

И, наконец, используя вычисленные значения 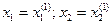, находим с помощью выражения (10.4) первое приближение для :

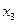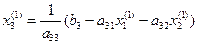. (10.7)

На этом заканчивается первая итерация решения системы (10.2-10.4). Используя теперь значения 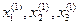можно таким же способом выполнить к решению 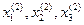и т.д. Приближение с номером К можно представить в виде:

,

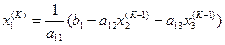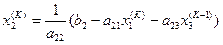, (10.8)

.

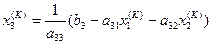Итерационный процесс выполняется до тех пор, пока значения 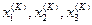не станут близкими к значениям 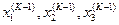с заданной погрешностью.