Метод хорд.

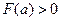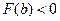Представлен на рисунке 12.1. Пусть известен отрезок [a,b], на котором функция меняет знак. Например , . В данном методе процесс итераций состоит в том, что в качестве приближения к корню уравнения 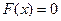принимаются значения 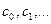точек пересечения хорды с осью абсцисс.

Сначала находим уравнение хорды АВ:

(12.1)

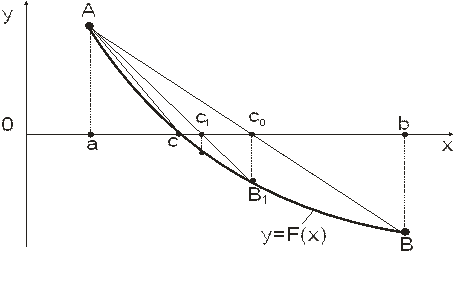
Рисунок 12.1 Метод хорд.

Для точки пересечения ее с осью абсцисс 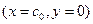получим уравнение

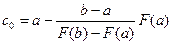(12.2)

Далее сравнивая знаки величин 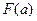и 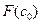для рассматриваемого случая, видим, что корень находится в интервале [a,с ], т.к. 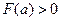, 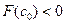. Отрезок [с ,b] отбрасываем.

Первая итерация состоит в определении нового приближения 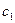, как точки пересечения хорды АВ 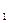с осью абсцисс. Итерационный процесс повторяется до тех пор, пока значение 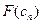не станет меньше по модулю заданного числа ε. 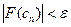. Этот метод всегда обеспечивает сходимость и более быстрый, чем предыдущий.

Блок-схема метода хорд подобна методу бисекций. Отличие в том, что корень вычисляется по формуле (12.2) и вводится оператор вычисления значений функций на границах отрезков.