Численные решения нелинейных уравнений.

В различных областях научных исследований встречаются задачи, для решения которых необходимо найти корни нелинейных уравнений вида .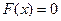

Существуют прямые и итерационные методы решения таких уравнений. Встречающиеся на практике нелинейные уравнения обычно не удается решить прямыми методами. Для решения таких задач оптимальными являются методы итераций, т.е. методы последовательных приближений.

Метод деления отрезка пополам (бисекции).

Это один из самых простых методов нахождения корней нелинейныхуравнений. Корень функций 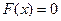находится в точке, при которой функция равна нулю. Допустим, имеется отрезок [a,b], в котором расположено искомое значение корня χ=c. Следовательно а<с<b. По этому методу в качестве начального приближения корня 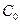принимается середина отрезка, т.е. 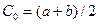. Далее исследуем значение функции на концах отрезков

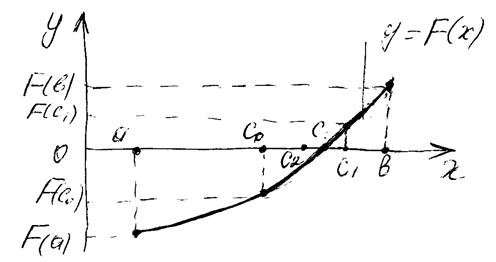
[a,с ] и [с ,b], т.е. в точках 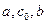,что видно из рисунка 11 1.

Рисунок 11. 1 Метод деления отрезка пополам.

Тот отрезок, на концах которого принимает значения разных знаков, содержит искомый корень, поэтому он принимается в качестве нового отрезка. Вторую половину, на которой знак функции не меняется, отбрасываем. В качестве первой итерации корня принимаем середину нового отрезка. Затем процесс повторяется. Таким образом, после каждой итерации отрезок, на котором расположен корень, уменьшается вдвое. После n итераций он уменьшится в 2 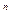раз.

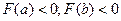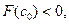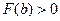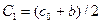На рис.11. 1 - это начальное приближение. Изменение знака происходит на отрезке [с ,b], т.к. а . Поэтому следующий отрезок для приближения будет [с ,b], а приближение . Теперь отрезок [с 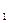,b] отбрасываем, т.к. 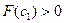и 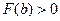. Искомый корень 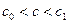. Затем аналогично находим 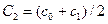и т.д. Итерационный процесс продолжается до тех пор, пока значение функции после n итераций не станет меньшим по модулю некоторого заданного малого числа ε, т.е. 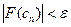. Можно ограничивать число итераций по длине отрезка, когда она станет меньше допустимой погрешности.

Блок-схема метода бисекций.

На рисунке 11.2 дана блок-схема итерационного метода бисекций. Нахождение корня уравнения 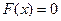. Здесь сужение отрезка производится путем замены границ а или b на текущее значение приближения корня с. При этом значение 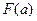вычисляется один раз, чтобы узнать знак функции на левой границе, и он в процессе итераций не меняется. Если знак 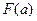и 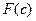совпадает, то левой границей становится первое приближение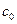 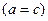и дальше 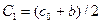. Если не совпадает, то левая граница остается а, но правая принимает значение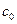 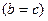и 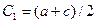. Затем цикл вычисления повторяется.

Метод бисекций довольно медленный, т.к. требует большого числа вычислений, но всегда сходится, причем с заданной точностью.

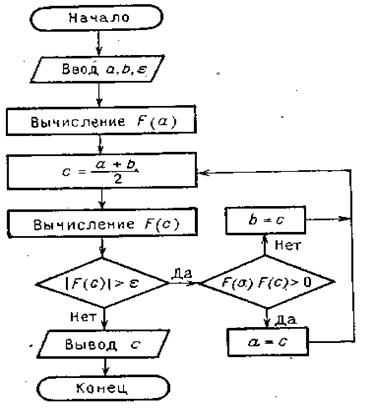
Рисунок 11.2 Блок-схема метода бисекций.