Определение момента инерции тела методом крутильных колебаний

Основными характеристиками динамики вращательного движения являются: момент инерции и момент силы.

Момент инерции– есть мера инертности тела, имеющего ось вращения.

Во вращательном движении момент инерции имеет такую же роль, как масса при поступательном движении. Как и масса момент инерции (относительно оси вращения) скалярная величина. Однако величина момента инерции тела зависит от положения оси вращения.

Момент инерции материальной точки относительно оси вращения, находящейся на расстоянии r, равен произведению массы на квадрат расстояния до оси вращения .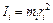

Момент инерции твердого тела равен сумме моментов инерции его составных точек 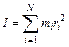. В случае непрерывного тела момент инерции тела относительно заданной оси представится выражением .

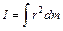Момент инерции относительно произвольной оси, не проходящей через центр масс, можно вычислить по теореме Штейнера.

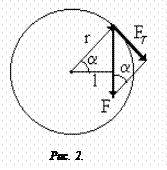
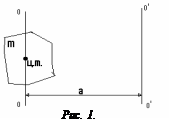Момент инерции относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс, параллельно заданной оси и произведению массы на квадрат расстояния между осями (рис.1).

I=I_o+ma². (1)

Момент силы – величина векторная, численно равная произведению силы на плечо

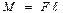. (2)

Плечом называется кратчайшее расстояние от оси вращения до линии действия силы (рис.2).

Момент силы и момент инерции связаны соотношением:

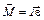,(3)

где ε – угловое ускорение.

Это есть основное уравнение динамики для вращательного движения.

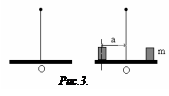Крутильные колебания – это такие колебания, которые совершает подвешенное твердое тело вокруг вертикальной невесомой упругой нити, верхний конец которой закреплен (рис.3).

Применим к этим колебаниям основное уравнение вращательного движения. При крутильных колебаниях на тело действует возвращающий момент со стороны нити подвеса, обусловленный упругими силам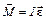и.

и ,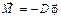

тогда

,

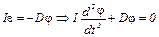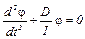. (4)

Полученное уравнение является дифференциальным уравнением крутильных колебаний, в этом уравнении отношение D/I = w² – циклическая частота – ω.

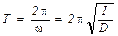. (5)

Вывод рабочей формулы.Воспользуемся методом крутильных колебаний для определения момента инерции диска, подвешенного на упругой нити (рис.4).

Для этого используем формулу периода крутильных колебаний. Однако в этой формуле две неизвестные величины: I – момент инерции диска относительно оси О, проходящей через центр масс диска, и D – модуль упругости нити.

Учитывая аддитивные свойства момента инерции, поставим на диск два груза и запишем второе уравнение

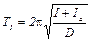, (6)

где I_a – момент инерции двух грузов относительно оси О. Возведем (5,6) в квадрат и разделим одно уравнение на другое:

, , .

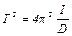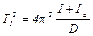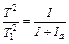Выразим момент инерции диска

.

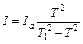Момент инерции двух грузов относительно оси О по теореме Штейнера равен:

,

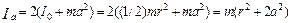где I₀ – момент инерции цилиндра относительно его оси, проходящей через центр масс. Подставим полученное выражение в предыдущую формулу и получим:

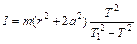, (7)

где r – радиус цилиндра, a – расстояние между осями диска и цилиндра.

Выражение (7) является рабочей формулой для расчета момента инерции диска.