Измерение ускорения силы тяжести с помощью оборотного маятника

Физический маятник – твердое тело, которое совершает колебания вокруг горизонтальной оси, не проходящей через центр масс (рисунок). В положении равновесия вращающий момент силы тяжести равен нулю, так как плечо этой силы равно нулю. При отклонении от положения равновесия на угол j (рисунок) возникает вращающий момент, равный

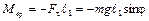. (1)

При малых углах (j »5⁰) sinj »j и тогда

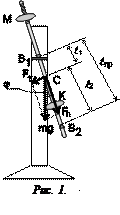
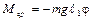. (2)

Минус означает, что вращающий момент стремится вернуть маятник в положение равновесия. Из основного уравнения динамики вращательного движения вращающий момент 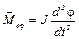, подставив в (2), получим

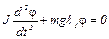. (3)

Выражение (3) называют дифференциальным уравнением колебаний физического маятника. В этом уравнении собственная циклическая частота колебаний физического маятника равна 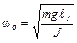. Период колебаний физического маятника

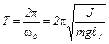. (4)

Если в формуле (4) вместо выражения 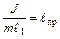подставим 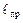, то получим формулу для периода математического маятника

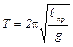, (5)

где 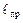– приведенная длина физического маятника. Эта величина показывает, что при длине математического маятника равной 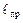_, периоды колебаний математического и физического маятника станут одинаковыми.

Точка, лежащая на прямой, проведенной через точку подвеса В₁ и центр тяжести С, на расстоянии приведенной длины 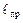от оси вращения, называется центром качания В₂. Если всю массу физического маятника сосредоточить в центре качания, то период его колебаний останется без изменений.

Точка подвеса В₁ и центр качания В₂ являются взаимозаменяемыми. Если маятник подвесить за центр качания или за точку подвеса, то периоды колебаний не изменятся. На этом свойстве основано измерение ускорения силы тяжести с помощью оборотного маятника (рис.1). Следует отметить, что при небольших смещениях подвижного груза М маятника, можно принять почти линейной зависимость периода колебаний маятника от положения груза.