Собственные векторы и собственные числа матрицы (линейного преобразования)

Пусть дано линейное преобразование

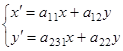(1)

с матрицей 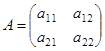. Будем под 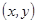понимать координаты точки или вектора, а под 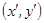соответственно координаты точки или вектора, полученных в результате преобразования.

Вектор 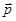отличный от нулевого называется собственным вектором матрицы , если в результате преобразования с матрицей он переходит в коллинеарный ему вектор , .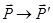

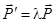Так, в преобразовании подобия все векторы собственные. В зеркальном отражении от оси 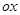собственными будут векторы параллельные оси 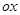. При повороте собственных векторов нет.

Число 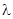называется собственным числом матрицы . Если 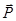– собственный вектор, то любой вектор, коллинеарный ему, тоже будет собственным. В самом деле, вектор 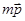перейдет в || || .

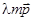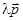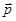Собственных векторов бесконечное множество. Они образуют направление, называемое инвариантным.

Найдем все собственные векторы линейного преобразования. Пусть дано линейное преобразование (1), вектор 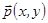– собственный для него и 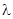– собственное число, т.е. 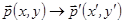и 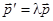. Тогда 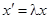, 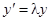. Или, подставляя в (1), получим

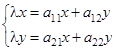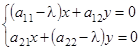или (2)

Это однородная система 2-х линейных уравнений с двумя неизвестными.

Если определитель системы не равен нулю, то система имеет единственное решение 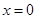и 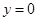, т.е. решением является лишь нулевой вектор, он собственным не является по определению. Значит, определитель

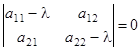(3)

И тогда система (2) имеет бесчисленное множество решений, а одно уравнение в (2) является следствием другого. Перепишем (3) в виде

(3')

Уравнение (3) или все равно (3'), называется уравнением собственных чисел матрицы преобразования . Так как это уравнение квадратное, то возможны случаи:

1) (3) имеет вещественные различные корн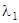и и 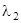. Подставляя 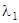в любое уравнение системы (2), получим

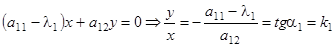– постоянное число

Это тангенс угла, образуемого собственным вектором 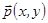с осью 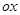. Он определяет инвариантное направление, соответствующее собственному числу 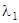матрицы .

Аналогично

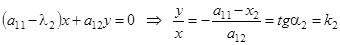
Получаем другое инвариантное направление.

2) Если уравнение(3) имеет равные корн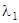и и 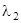, то инвариантное направление одно.

3) Если уравнение (3) не имеет действительных корней (они комплексные), то преобразование не имеет инвариантных направлений.

Замечание. В случае преобразования подобия уравнение (3) имеет вид

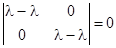
Поэтому любое направление есть инвариантное.