Решение систем линейных уравнений с помощью обратной матрицы
Пусть дана система 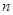 линейных уравнений с
линейных уравнений с 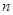 неизвестными.
неизвестными.
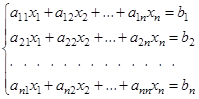 (1)
(1)
Обозначим 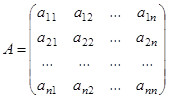 матрицу из коэффициентов, через
матрицу из коэффициентов, через 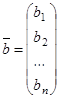 матрицу-столбец свободных членов, через
матрицу-столбец свободных членов, через 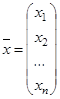 матрицу-столбец из неизвестных. Тогда система (1) кратко может быть записана в виде матричного уравнения
матрицу-столбец из неизвестных. Тогда система (1) кратко может быть записана в виде матричного уравнения 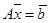 . (2)
. (2)
Пусть матрица  неособенная, т.е.
неособенная, т.е. 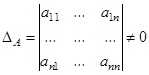 . Тогда существует обратная матрица
. Тогда существует обратная матрица 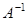 .
.
Умножим обе части уравнения (2) слева на матрицу 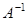 , получим
, получим
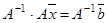 или
или 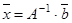 (3),
(3),
что и дает решение системы (1).
Пример.
Решить систему уравнений:
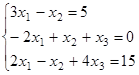
Решение.
Запишем систему в матричной форме.
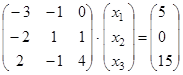
Определитель
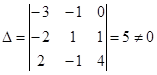
Вычислим обратную матрицу 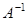 :
: 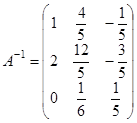 , отсюда
, отсюда 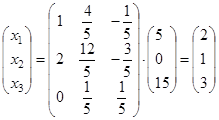 .
.
Значит: 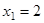 ,
, 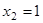 ,
, 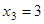 .
.
Замечание. Нетрудно видеть, что матричная формула (3) может быть записана в виде 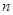 формул
формул 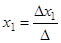 ,
, 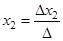 , ...,
, ..., 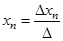 – Формулы Крамера. Здесь
– Формулы Крамера. Здесь 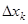 получается из
получается из 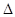 заменой k-го столбца столбцом свободных членов
заменой k-го столбца столбцом свободных членов 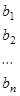 .
.
Дата добавления: 2015-10-05; просмотров: 856;
