Понятие ранга матрицы
Пусть дана прямоугольная матрица
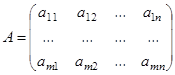 .
.
Если в ней выбрать произвольно 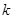 столбцов и
столбцов и 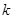 строк (
строк ( 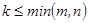 ), то элементы, стоящие на пересечении этих строк и столбцов, образуют квадратную матрицу порядка
), то элементы, стоящие на пересечении этих строк и столбцов, образуют квадратную матрицу порядка 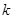 . Определитель этой матрицы называется минором k-го порядка матрицы
. Определитель этой матрицы называется минором k-го порядка матрицы  .
.
Определение 1. Рангом матрицы  называется максимальный порядок минора матрицы, отличного от нуля, т.е.
называется максимальный порядок минора матрицы, отличного от нуля, т.е.  имеет ранг
имеет ранг 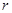 , если
, если
1) найдется хоть один минор в  порядка
порядка 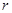 , отличный от нуля;
, отличный от нуля;
2) все миноры порядка 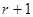 и выше равны 0. Символически обозначают
и выше равны 0. Символически обозначают 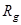 . Минор порядка
. Минор порядка 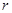 называется базисным минором матрицы. Матрица может иметь и несколько базисных миноров, но они все имеют одинаковый порядок
называется базисным минором матрицы. Матрица может иметь и несколько базисных миноров, но они все имеют одинаковый порядок 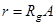 .
.
Практически вычисляют миноры с первого порядка и выше по порядку. Если найден минор r-ого порядка неравный нулю, то оказывается достаточно вычислить лишь миноры 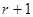 порядка, содержащие его. Если они равны нулю все, то ранг матрицы равен
порядка, содержащие его. Если они равны нулю все, то ранг матрицы равен 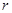 . Если хоть один не равен нулю, то операцию применяют к нему.
. Если хоть один не равен нулю, то операцию применяют к нему.
Пример.
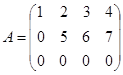
Есть миноры 1-ого и 2-ого порядков неравные нулю. А все третьего – равны нулю, так как содержат строку из нулей. Значит, 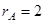 .
.
Однако прямое вычисление миноров матрицы очень трудоемко. Поэтому матрицу предварительно преобразуют.
Определение 2. Под элементарным преобразованием матрицы понимают следующие операции:
1) умножение какой-либо строки (столбца) матрицы на число неравное нулю;
2) прибавление к элементам какой-либо строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число;
3) перестановка двух строк (двух столбцов) матрицы.
Справедлива теорема. При элементарном преобразовании ранг матрицы не меняется.
Эту теорему используют для практического вычисления ранга матрицы. Стараются сначала преобразовать матрицу так, чтобы в ней было побольше нулей, а затем уже определяют ранг.
Довольно часто при этом матрица  приводится к виду
приводится к виду
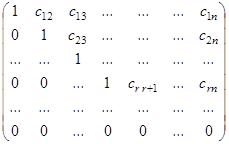 .
.
Эта матрица называется трапециевидной.
Например.
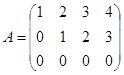
Есть трапециевидная. Как видим, ее ранг легко вычисляется 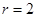 .
.
Треугольная матрица
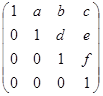 – частный случай трапециевидной.
– частный случай трапециевидной. 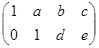 тоже трапециевидная.
тоже трапециевидная.
Оказывается любую матрицу  при помощи элементарных преобразований над строчками и перестановок столбцов можно сделать трапециевидной.
при помощи элементарных преобразований над строчками и перестановок столбцов можно сделать трапециевидной.
Пример.
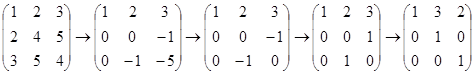 ,
, 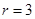 .
.
Дата добавления: 2015-10-05; просмотров: 1409;
