Основные определения. Действия над матрицами

Определение 1. Система 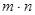чисел, расположенных в прямоугольной таблице из 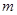строк и 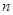столбцов,

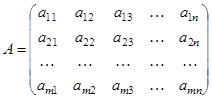, (1)

называется матрицей. Строки и столбцы называются рядами матрицы.

Числа 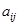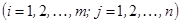, составляющие матрицу, называются ее элементами. Здесь первый индекс 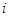означает номер строки элемента, а второй 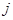– номер его столбца.

Для матрицы (1) употребляют и сокращенную запись 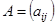( 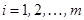; 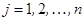) или 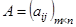. При этом говорят, что матрица имеет тип .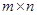

Если 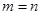, то матрица называется квадратной порядка 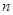, если же 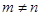, то матрица называется прямоугольной. Определитель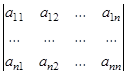

называется определителем квадратной матрицы . В частности, матрица может состоять из одного числа, это матрица типа 1´1: 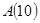, может состоять из одной строки или одного столбца:

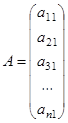и .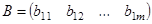

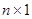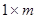Их типы и соответственно. Квадратная матрица вида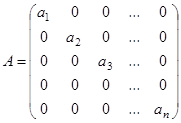

называется диагональной и обозначается кратко 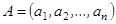. Если все 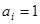в диагональной матрице, то она называется единичной и обозначается буквой 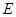. Итак, .

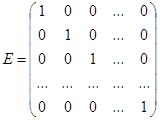Квадратная матрица называется симметрической, если элементы матрицы, симметрично расположенные относительно главной диагонали, равны между собой. Матрица, все элементы которой равны 0, называется нулевой матрицей и обозначается буквой 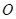. Если нужно подчеркнуть тип, то пишут .

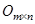Рассмотрим действия над матрицами.

Определение 2. Матрицы 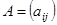и 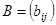считаются равными, если они одного типа, и соответствующие элементы их равны, т.е. .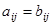

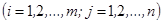Определение 3. Суммой (разностью) матриц 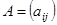и 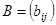одинакового типа называется матрица 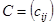того же типа, элементы которой равны суммам (разностям) соответствующих элементов матриц и 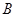, т.е. .

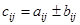Пример.

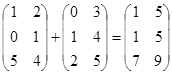
Очевидно выполнение свойств:

1) ,

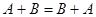2) ,

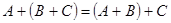3) .

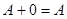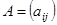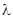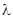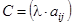Определение 4. Произведение матрицы на число (или, все равно, числа на матрицу ) называется матрица , т.е. все элементы которой получены из соответствующих элементов умножением на число .

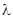Пример.

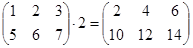
Из определения очевидны свойства:

1) ,

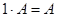2) ,

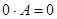3) ,

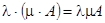4) ,

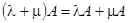5) .

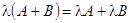Определим умножение двух матриц. Пусть даны матрицы 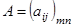и 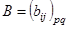. Причем, пусть число столбцов матрицы равно числу строк матрицы 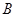, т.е. .

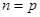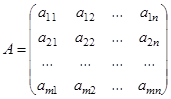и

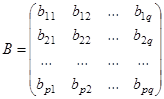
Определение 5. Произведением матриц и 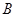называется матрица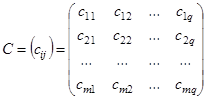

типа 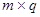, каждый элемент которой получается как сумма произведений элементов 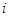-ой строки матрицы на соответствующие элементы 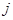-ого столбца матрицы : .

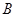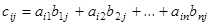
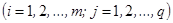Из определения следует, что квадратные матрицы можно перемножать лишь одного порядка.

Пример.

, ,

.

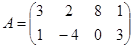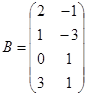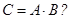
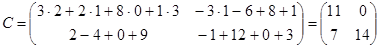Справедливы свойства:

1) ,

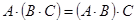2) ,

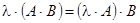3) ,

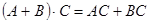4) .

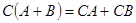Произведение двух матриц не обладает переместительным свойством, т.е. .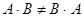

Пример.

, .

, . .

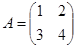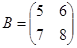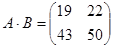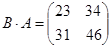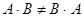Более того, может быть, что произведение 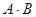существует, а 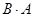не имеет даже смысла.

Пример.

, . .

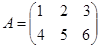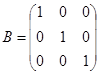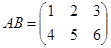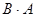не существует, так как число столбцов в 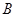больше числа строк в .

Если 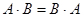, то матрицы и 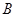называются перестановочными или коммутативными. Например, единичная матрица 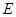перестановочна с любой квадратной матрицей того же порядка. 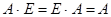, т.е. 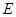играет роль единицы при умножении.