Уравнение эллипса.

Можно показать (мы этого не делаем), что уравнение (2) равносильно уравнению (1), хотя оно и получено из (1) путем неэквивалентных преобразований. Это и означает, что уравнение (2)—уравнение данного эллипса. Оно называется каноническим (т.е. наиболее простым).

Видно, что уравнение эллипса есть уравнение 2-ого порядка, т.е. эллипс—линия 2-го порядка.

Для эллипса введем понятие эксцентриситет.Это величина 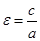. Для эллипса эксцентриситет 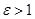. Так как с и а известны, то 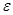тоже известен. Выражение фокальных радиусов точки М(х, у) эллипса легко получаем из предыдущих рассуждений: 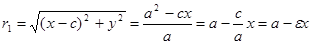. r₂ найдем из равенства 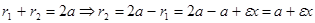(3)

Замечание Если в стол вбить два гвоздя (F1 и F2), привязать к ним обоими концами шнурок, длина которого больше расстояния между гвоздями (2а), натянуть шнур и куском мела вести по столу, то он вычертит замкнутую кривую—эллипс, которая симметрична относительно обеих осей и начала координат.

4. Исследование формы эллипса по его каноническому уравнению.

В замечании мы из соображений наглядности сделали вывод о форме эллипса. Проведем теперь исследование формы эллипса, анализируя его каноническое уравнение: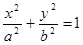

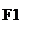
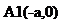
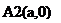
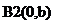
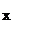
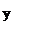
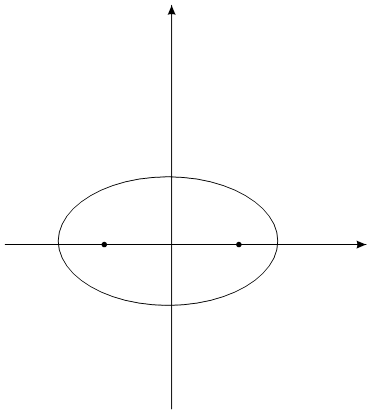
Найдем точки пересечения с осями координат. Если 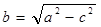,у=0, то 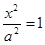, , 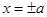т.е. имеем две точки А1(-а,0) и А2(а,0). Если х=0, то 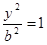, 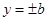. Т.е. имеем две точки В1(0,-b) и B2(0,b) (т.к. 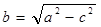, то 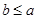). Точки А1,А2,В1,В2 называют вершинами эллипса.

2) Область расположения эллипса можно определить из следующих соображений:

а) из уравнения эллипса следует, что 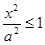, т.е. 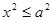, т.е. 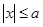или .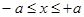

б) аналогично 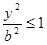, т.е. 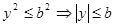или 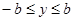. Это показывает, что весь эллипс расположен в прямоугольнике, образованном прямым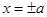и и .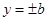

3) Далее, в уравнение эллипса переменные х и у входят только в четных степенях, а это означает, что кривая симметрична относительно каждой из осей и относительно начала координат. Д-но, если радиусу принадлежит точка (х, у), то ему принадлежат и точки (х, -у), (-х, у) и (-х, -у). Поэтому достаточно рассмотреть лишь ту часть эллипса, которая лежит в первой четверти, где 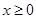и .

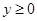4) Из уравнения эллипса имеем 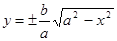, а в первой четверти 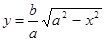. Если х=0, то у=b. Это есть точка B2(0,b). Пусть х увеличивается от 0 до а, тогда y уменьшается от b до 0. Тем самым точка М(х, у), начиная из точки В2(0, b) описывая дугу приходит в точку А(а,0). Можно строго доказать, что дуга выпуклостью направлена вверх. Отражая зеркально эту дугу в осях координат и начале, мы и получим весь эллипс. Оси симметрии эллипса называются его осями, точка О пересечения их—центром эллипса. Длину отрезков ОА1=ОА2=а называют большой полуосью эллипса, отрезков ОВ1,ОВ2=b—малой полуосью эллипса, (а>b), c—полуфокусным расстоянием. Величину 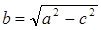просто пояснить геометрически.

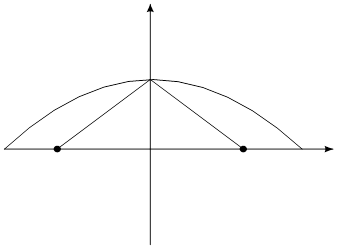
При а=b получаем из канонического уравнения эллипса 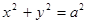--уравнение окружности. Для окружности 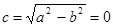, т.е. F1=F2=0. .

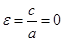Таким образом, окружность—это частный случай эллипса, когда фокусы его совпадают с центром и эксцентриситет=0. Чем больше эксцентриситет, тем больше вытянут эллипс.

Замечание. Из канонического уравнения эллипса легко заключить, что эллипс можно задать в параметрической форме. x=a cos t

y=b sin t, где a, b –большая и малая полуоси, t—угол.

5. Определение и вывод канонического уравнения гиперболы.

Гиперболой называется ГМТ плоскости, для которых разность расстояний от двух фиксированных точек F1F2 плоскости, называемых фокусами, есть постоянная величина (не равная 0 и меньшая, чем фокусное расстояние F1F2).

Будем обозначать, по-прежнему, F1F2=2с, а разность расстояний—2а (а<с). Систему координат выберем как и в случае эллипса.

Пусть М (х,у)—текущая точка гиперболы. По определению МF1-MF2= 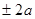или r₁-r₂= = 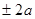или 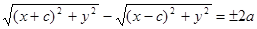--(1). –это и есть уравнение гиперболы.

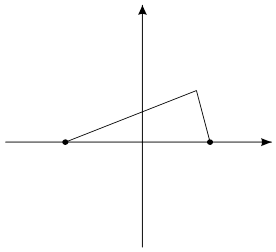
Избавляемся от иррациональности в (1): уединим один корень, возведем обе части в квадрат, получим: 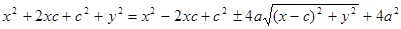или 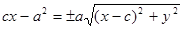, снова возведем в квадрат: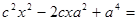

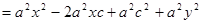, откуда .

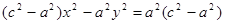Разделим на 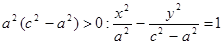. Введем обозначение 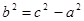. Тогда 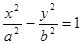--(2). Уравнение (2), как можно показать, равносильно уравнению (1), а потому есть уравнение данной гиперболы. Его называют каноническим уравнением гиперболы. Видим, что уравнение гиперболы тоже второй степени, значит, гипербола—линия второго порядка.

Эксцентриситет гиперболы 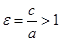. Выражение фокальных радиусов через 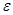легко получить из предыдущего 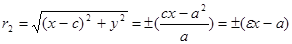, тогда 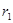находим из .

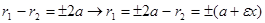6. Исследование формы гиперболы по ее каноническому уравнению.

Рассуждаем аналогично тому, как при исследовании эллипса.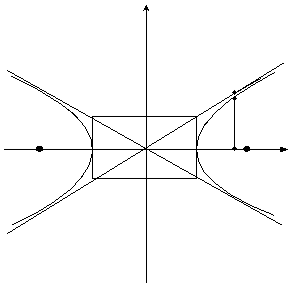

1. Находим точки пересечения с осями гиперболы. Если х=0, то 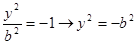. Точек пересечения с осью ОУ нет. Если у=0, то 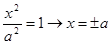. Точки пересечения 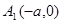, 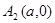. Они называются вершинами гиперболы.

2. Область расположения гиперболы: 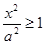, т.е.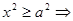 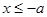или 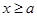. Значит, гипербола расположена вне полосы, ограниченной прямыми x=-a и х=а.

3. Гипербола обладает всеми видами симметрии, т.к. х и у входят в четных степенях. Поэтому достаточно рассмотреть ту часть гиперболы, которая расположена в первой четверти.

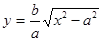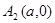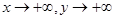4. Из уравнения гиперболы (2) в первой четверти имеем . При х=а, у=0 имеем точку ; при , т.е. кривая уходит вправо вверх. Чтобы ход представить яснее, рассмотрим две вспомогательные прямые, проходящие через начало координат и являющиеся диагоналями прямоугольника со сторонами 2а и 2b: BCB’C’. Они имеют уравнения 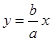и 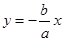. Докажем, что текущая точка гиперболы М(х,у) уходя в бесконечность неограниченно приближается к прямой 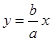. Возьмем произвольную точку х и сравним соответствующие ординаты точки гиперболы 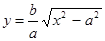и 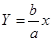--прямой. Очевидно, что У>у. MN=Y-y= .

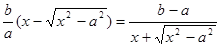Видим, что при 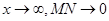, т.е. кривая неограниченно приближается к прямой по мере удаления от начала координат. Это доказывает, что прямая является асимптотой гиперболы. Причем гипербола не пересекает асимптоту. Этого достаточно, чтобы построить часть гиперболы. Она обращена выпуклостью вверх. Остальные части достраиваются по симметрии. Заметим, что оси симметрии гиперболы (оси координат) называются ее осями, точка пересечения осей—центром гиперболы. Одна ось пересекает гиперболу (действительная ось), другая—нет (мнимая). Отрезок а называют действительной полуосью, отрезок b—мнимой полуосью. Прямоугольник BCB’C’—называется основным прямоугольником гиперболы.

Если а=b, то асимптоты образуют с осями координат углы по 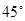. Тогда гиперболу 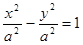или 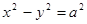называют равносторонней или равнобочной. Основной прямоугольник превращается в квадрат. Асимптоты ее перпендикулярны друг другу.

Замечание.

Иногда рассматривают гиперболу, каноническое уравнение которой 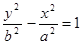--(3). Ее называют сопряженной по отношению к гиперболе (2). Гипербола (3) имеет действительную ось вертикальную, мнимую—горизонтальную. Ее вид сразу устанавливается, если переставить х и у, а и b (она превращается в прежнюю). Но тогда гипербола (3) имеет вид:

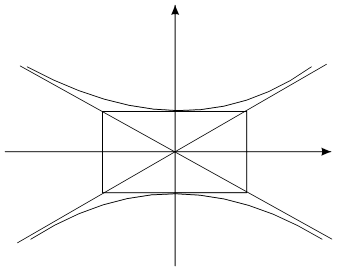
Вершины ее .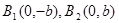

5.Как уже указывалось, уравнение равносторонней гиперболы (а=b), когда оси координат совпадают с осями гиперболы, имеет вид 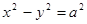. (4)

Т.к. асимптоты равносторонней гиперболы перпендикулярны, то их тоже можно взять за оси координат ОХ₁ и ОУ₁. Это равносильно повороту прежней системы ОХУ на угол 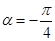. Формулы поворота на угол 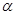следующие:

,

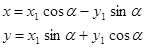при .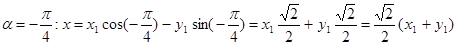

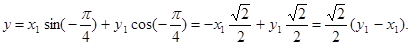
Тогда в новой системе координат ОХ₁У₁ уравнение (4) перепишется:

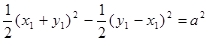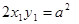или или 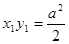. Обозначая 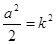, получим 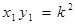или 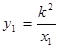(5)—это уравнение равносторонней гиперболы, отнесенной к асимптотам (именно этот вид гиперболы рассматривался в школе).

Замечание: Из уравнения 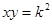следует, что площадь любого прямоугольника, построенного на координатах любой точки гиперболы М(х,у) одна и та же: S=k².

7. Определение и вывод канонического уравнение параболы.

Параболойназывается ГМТ плоскости, для каждой из которых расстояние от фиксированной точки Fплоскости, называемой фокусом, равно расстоянию от фиксированной прямой, называемой директрисой (фокус вне директрисы).

Будем обозначать расстояние от Fдо директрисы через р и называть параметром параболы. Выберем следующим образом систему координат: ось ОХ проведем через точку Fперпендикулярно директрисе NP. Начало координат выберем в середине отрезкаFP.

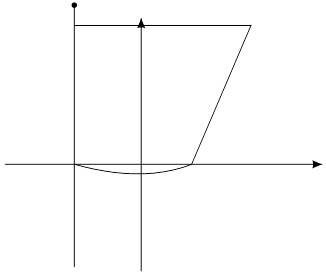В этой системе: .

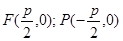Возьмем произвольную точку М(х,у) с текущими координатами (х,у). Поэтому

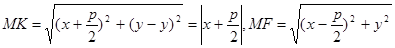. Отсюда 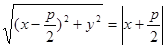(1)—это и есть уравнение параболы. Упростим:

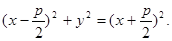
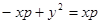или 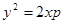(2)—это и есть каноническое уравнение параболы. Можно показать, что (1) и (2) равносильны.

Уравнение (2) есть уравнение 2-го порядка, т.е. парабола—линия 2-го порядка.

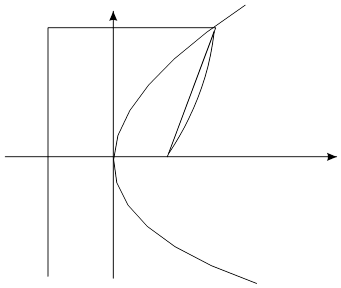
8. Исследование формы параболы по ее каноническому уравнению.

(р>0).

[КИ1]

1) х=0, у=0 парабола проходит через начало координат точку О. Ее называют вершиной параболы.

2) 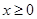, т.е. парабола располагается правее оси ОУ, в правой полуплоскости.

3) у входит в четной степени, потому парабола симметрична относительно оси ОХ, следовательно, достаточно построить в первой четверти.

4) в 1 четверт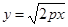и при 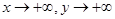, т.е. парабола идет вверх вправо. Можно показать, что выпуклостью—вверх. По симметрии строим внизу. Ось ОУ—касательная к параболе.

Очевидно, фокальный радиус-- 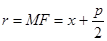. Отношение 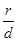называется эксцентриситетом: 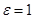. Ось симметрии параболы (у нас ОХ) называется осью параболы.

Заметим, что уравнение 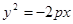тоже есть парабола, но направленная в противоположную сторону. Уравнения 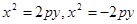тоже задают параболы, осью которых является ось ОУ.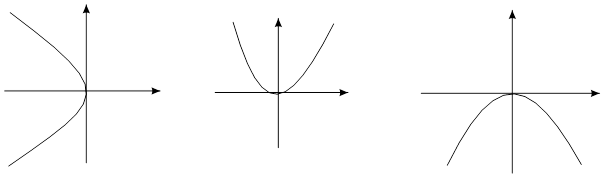

или в более привычном ви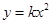де , где .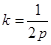

Уравнение 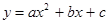определяет обычную параболу со смещенной вершиной .

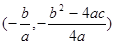Замечания. 1) Между всеми четырьмя линиями 2-го порядка существует близкое родство—все они являются коническими сечениями. Если взять конус из двух полостей, то при сечении плоскостью перпендикулярной оси конуса получим окружность, если чуть наклонить плоскость сечения получим эллипс; если плоскость параллельна образующей, то в сечении—парабола, если плоскость пересекает обе

полости—гипербола.

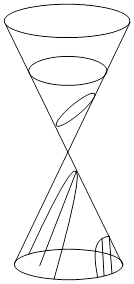
2) Можно доказать, что если луч света исходя из фокуса параболы, отражается от нее, то отраженный луч идет параллельно оси параболы—это используется при действии прожекторов—параболический отражатель, а в фокусе—источник света. Получается направленный поток света.

3) Если представить запуск спутника Земли из точки Т, лежащей за пределами атмосферы в горизонтальном направлении, то если начальная скорость v₀ недостаточна, то спутник вращаться вокруг Земли не будет. При достижении 1-ой космической скорости спутник будет вращаться вокруг Земли по круговой орбите с центром в центре Земли. Если начальную скорость увеличить, то вращение будет происходить по эллипсу, центр Земли будет в одном из фокусов. При достижении 2-ой космической скорости траектория станет параболической и спутник не вернется в точку Т, но будет находиться в пределах Солнечной системы. Т.е. парабола есть эллипс с одним бесконечно удаленным фокусом. При дальнейшем увеличении начальной скорости траектория станет гиперболической и второй фокус появиться с другой стороны. Центр Земли будет все время находиться в фокусе орбиты. Спутник уйдет за пределы Солнечной системы.