Понятие об обратной матрице
Определение 1. Обратной матрицей по отношению к данной называется матрица, которая будучи умноженной справа (или слева) на данную матрицу, дает единичную матрицу.
Матрицу, обратную к матрице  , обозначают
, обозначают 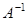 . По определению
. По определению 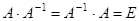 .
.
Определение 2. Матрица называется неособенной, если: 1) она квадратная; 2) ее определитель отличен от нуля.
Справедлива теорема. Всякая неособенная матрица имеет обратную матрицу (без доказательства).
Практически, если дана неособенная матрица
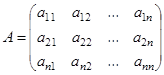 , т.е.
, т.е. 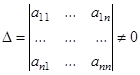 , то
, то 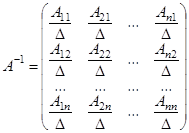 ,
,
где 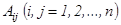 есть алгебраические дополнения (миноры со знаками) соответствующих элементов
есть алгебраические дополнения (миноры со знаками) соответствующих элементов 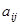 . Следует заметить, что при составлении матрицы
. Следует заметить, что при составлении матрицы 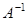 алгебраические дополнения для элементов
алгебраические дополнения для элементов 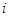 -ой строки матрицы
-ой строки матрицы  записываются в
записываются в 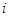 -ом столбце матрицы
-ом столбце матрицы 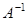 (транспонируются).
(транспонируются).
Пример.
Для матрицы 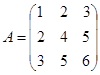 найти обратную
найти обратную 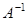 .
.
Определитель 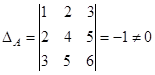 , т.е.
, т.е.  неособенная.
неособенная. 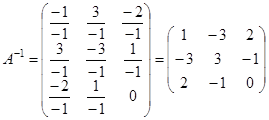 .
.
Оказываются справедливы свойства:
1) Определитель обратной матрицы равен обратной величине определителя исходной матрицы.
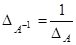
2) Обратная матрица произведения равна произведению обратных матриц сомножителей, взятому в обратном порядке.
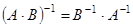
Дата добавления: 2015-10-05; просмотров: 890;
