Линейные преобразования на плоскости и в пространстве

Если задано правило, по которому каждой точке 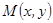плоскости ставится в соответствие точка 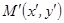той же плоскости, то говорят, что задано преобразование плоскости: .

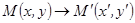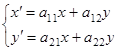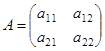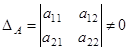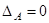Если при этом , то это преобразование называется линейным. Оно характеризуется матрицей . Если определитель матрицы (т.е. матрица неособенная), то линейное преобразование называется невырожденным (или афинным). Если , то преобразование вырожденное.

Аналогично определяется линейное преобразование в пространстве. В этом случае

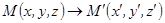и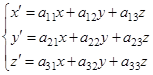

Матрица 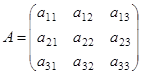– матрица преобразования.

Примеры.

1) Поворот на угол .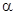

.

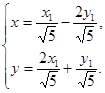
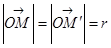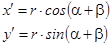
или после преобразования

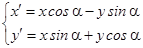
преобразование линейное.

Матрица преобразования

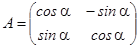
Определитель 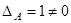, т.е. преобразование невырожденное, афинное.

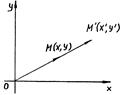
1) Преобразование подобия

Пусть 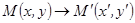,причем 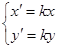линейное преобразование.

Матрица .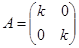

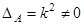преобразование афинное.

1) Зеркальное отражение от оси .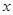

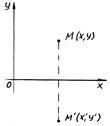
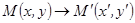
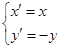
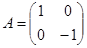
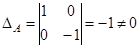преобразование афинное.

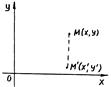
1) Проектирование на ось .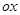

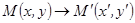
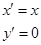
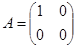
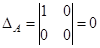преобразование линейное, вырожденное.

Плоскость преобразуется в прямую.