Собственные числа и собственные векторы в случае симметрической матрицы
Пусть 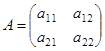 – матрица преобразования и пусть она симметрическая, т.е.
– матрица преобразования и пусть она симметрическая, т.е. 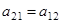 , тогда
, тогда 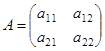 .
.
Из уравнения (3') имеем
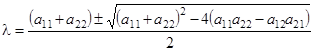 .
.
Так как у нас 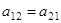 , то
, то
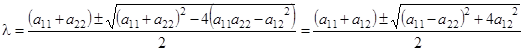
Так как 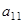 ,
, 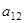 ,
, 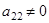 одновременно, то отсюда следует:
одновременно, то отсюда следует:
1) подкоренное выражение 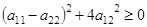 , т.е. симметрическая матрица имеет всегда вещественные собственные числа
, т.е. симметрическая матрица имеет всегда вещественные собственные числа 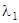 и
и 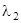 .
.
2) Эти вещественные собственные числа различны, т.е. 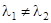 . Если бы
. Если бы 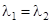 , то
, то 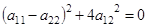 и матрица
и матрица 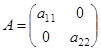 , имели бы
, имели бы  , т.е. имели бы преобразование подобия, что совсем необязательно (у нас произвольное линейное преобразование).
, т.е. имели бы преобразование подобия, что совсем необязательно (у нас произвольное линейное преобразование).
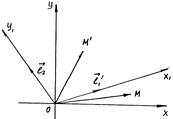
Теорема. Инвариантные направления симметричной матрицы взаимно перпендикулярны.
Доказательство.
Как уже отмечали  – первое инвариантное направление,
– первое инвариантное направление,  – второе инвариантное направление.
– второе инвариантное направление.

Из уравнения (3') по теореме Виета и учитывая, что 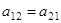 , получаем
, получаем  ,
, 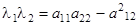 .
.
Тогда  ,
,  ,
, 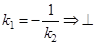 -ть направлений.
-ть направлений.
|
Примем инвариантные направления симметрической матрицы преобразования за новые оси координат, обозначив их 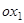 и
и 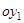 .
. 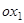 соответствует собственному числу
соответствует собственному числу 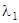 ,
, 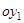 соответствует собственному числу
соответствует собственному числу 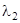 .
.
В старой системе координат 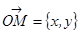 ,
,  ,
,  .
.

В новой системе  ,
, 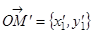 ,
,  .
.
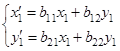 (1)
(1)
Найдем матрицу преобразования в новой системе координат.

Возьмем вектор  , лежащий на оси
, лежащий на оси 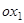 . Он лежит на инвариантном направлении, соответствующем числу
. Он лежит на инвариантном направлении, соответствующем числу 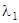 . Поэтому он перейдет в вектор
. Поэтому он перейдет в вектор 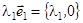 .
.
Получаем
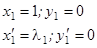 .
.
Подставляем в (1), получим  ,
, 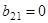 .
.
Возьмем вектор  , лежащий на другом инвариантном направлении. Он перейдет в вектор
, лежащий на другом инвариантном направлении. Он перейдет в вектор 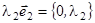 .
.
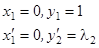
Подставляя в (1), получим  ,
,  .
.
Окончательно (1) перепишется в виде 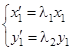 (2).
(2).
Вывод: Если инвариантные направления симметрической матрицы линейного преобразования  принять за оси координат, то эта матрица приобретает диагональный вид
принять за оси координат, то эта матрица приобретает диагональный вид 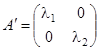 .
.
Дата добавления: 2015-10-05; просмотров: 950;
