Приведение квадратичной формы к каноническому виду

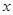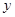Рассмотрим квадратичную форму от двух переменных и , т.е. однородный многочлен второй степени относительно 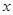и 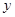: 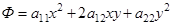. Ее можно записать в виде .

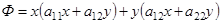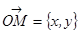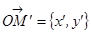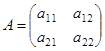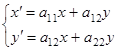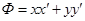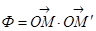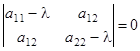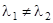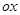Рассмотрим линейное преобразование , где , , причем, матрица этого преобразования симметрическая . Тогда имеем . Квадратичная форма перепишется , т.е. – скалярное произведение. Как мы видели, уравнение собственных чисел для симметрической матрицы имеет два различных действительных корня , и им соответствуют два различных инвариантных направления линейного преобразования: , – угол наклона к оси первого инвариантного направления, и 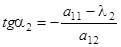, 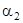– второго инвариантного направления. Они перпендикулярны.

Возьмем эти инвариантные направления за новые оси координат 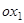и 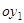, но так, чтобы система получилась правой, т.е. кратчайший поворот от положительного направления оси 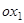к 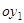был против часовой стрелки. 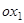соответствует собственному числу 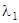, 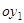соответствует собственному числу 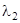. В новых координатах , 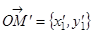. Но 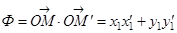. Как установлено выше, матрица преобразования в новых координатах имеет диагональный вид 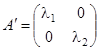, поэтому 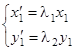, и потому 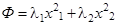– этот вид квадратичной формы и называется каноническим, квадратичная форма содержит лишь квадраты текущих координат и не содержит их произведения.