Приведение общего уравнения второго порядка к каноническому виду
Общее уравнение второго порядка имеет вид
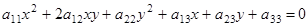
С помощью преобразования поворота
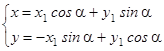 на угол
на угол 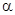 и параллельного переноса
и параллельного переноса 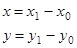 общее уравнение может быть преобразовано к одному из следующих основных видов:
общее уравнение может быть преобразовано к одному из следующих основных видов:
1)  – эллипс;
– эллипс;
2) 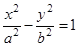 – гипербола;
– гипербола;
3)  или
или  – парабола;
– парабола;
4)  – две пересекающиеся прямые;
– две пересекающиеся прямые;
5)  или
или 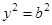 – две параллельные прямые.
– две параллельные прямые.
Если координатные оси новой системы 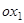 и
и 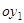 направить по двум инвариантным направлениям (повернуть систему на угол
направить по двум инвариантным направлениям (повернуть систему на угол 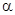 ), соответствующим собственным числам
), соответствующим собственным числам 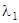 и
и 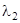 матрицы
матрицы 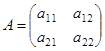 , то квадратичная форма из трех старших членов
, то квадратичная форма из трех старших членов 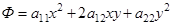 примет канонический вид
примет канонический вид  . Группа членов первой степени преобразуется в подобную же группу
. Группа членов первой степени преобразуется в подобную же группу
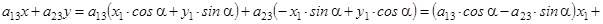
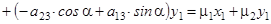
Свободный член не изменится.
Полученное уравнение 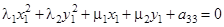 упрощаем далее, производя параллельный перенос осей, в результате чего исчезают члены с первыми степенями координат. Получаем уравнение вида
упрощаем далее, производя параллельный перенос осей, в результате чего исчезают члены с первыми степенями координат. Получаем уравнение вида 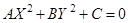 , которое и называется каноническим видом уравнения второго порядка. На сколько нужно параллельно переносить оси решается в каждом примере особо (хотя есть и общая теория).
, которое и называется каноническим видом уравнения второго порядка. На сколько нужно параллельно переносить оси решается в каждом примере особо (хотя есть и общая теория).
Пример.
Привести к каноническому виду уравнение 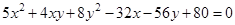 .
.
Решение.
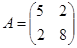 . Уравнение собственных чисел
. Уравнение собственных чисел 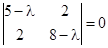 ,
, 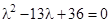
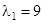 ,
,  .
.
Возьмем за первое инвариантное направление то, тангенс которого положителен, т.е. которое образует с осью  острый угол. В данном случае
острый угол. В данном случае 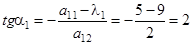 . Направление составляет с осью
. Направление составляет с осью 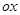 угол
угол 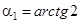 , его берем за ось
, его берем за ось 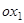 . Второе направление берем за
. Второе направление берем за 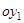 так, чтобы оно было перпендикулярно первому и составляло правую систему с
так, чтобы оно было перпендикулярно первому и составляло правую систему с 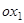 . Тогда
. Тогда  .
.
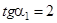 ,
, 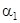 – острый угол,
– острый угол, 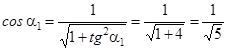 ,
, 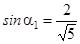 .
.
Система  повернута на угол
повернута на угол 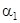 , поэтому формулы преобразования будут
, поэтому формулы преобразования будут
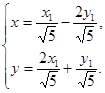 (*)
(*)
Поворот системы oxy на 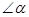 ,равносилен повороту радиуса-вектора на угол(-
,равносилен повороту радиуса-вектора на угол(- 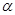 ),поэтому
),поэтому

Остальные члены данного уравнения преобразуются:
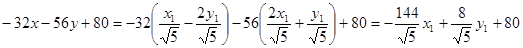 .
.
Исходное уравнение в системе 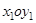 запишется:
запишется:
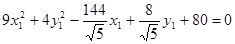 .
.
Выделим в нем полные квадраты по  и
и 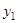 :
:
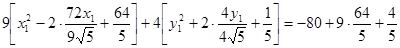
или
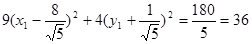 .
.
Совершим теперь параллельный перенос системы 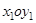 по формулам
по формулам 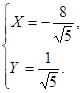 Найдем координаты нового начала
Найдем координаты нового начала  :
: 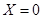 ,
,  в последний системе координат
в последний системе координат  . В системе
. В системе  координаты нового начала
координаты нового начала  будут, очевидно:
будут, очевидно: 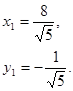
Используя формулы (*), получаем:
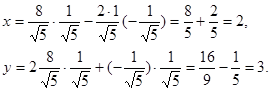
Итак, новое начало  в исходной системе будет:
в исходной системе будет: 
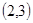 .
.
Уравнение данной кривой в последней системе координат  будет иметь вид:
будет иметь вид: 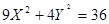 или
или 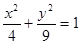 .
.
Это эллипс с полуосями 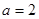 ,
, 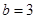 .
.
Построим чертеж:
1) Строим систему  .
.
2) Строим первое инвариантное направление под углом 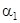 (
( 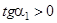 ) и берем его за ось
) и берем его за ось 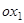 . Ось
. Ось 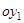 строим перпендикулярно и направляем так, чтобы система
строим перпендикулярно и направляем так, чтобы система 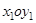 была правой.
была правой.
3) Наносим на чертеж точку 
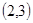 .
.
4)
 |
Переносим в точку
 начало системы
начало системы 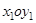 , сохраняя параллельность (направление) осей, получим систему
, сохраняя параллельность (направление) осей, получим систему 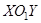 .
.
5) Строим в этой системе эллипс.
Дата добавления: 2015-10-05; просмотров: 2415;
