Сжатие и растяжение поверхностей.

Пусть имеем некоторую поверхность 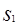, F(x,y,z)=0 (1)- её уравнение. Возьмём какое-либо положительное число к>0 и заменим каждую точку 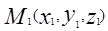поверхности 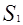другой точкой М(х,у,z) причём, , , .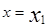

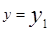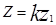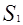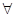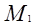Тогда поверхность преобразуется в новую поверхность S. Очевидно, при к>1 имеем растяжение в направлениях оси OZ , в случае k<1 -сжатие по той же оси. Точка лежит на поверхности .

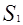Поэтому 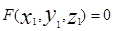или 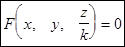(2). Уравнению (2) удовлетворяет координаты любой точки М на S. Значит, (2) и есть уравнение «растянутой» по оси OZ поверхности S.

Итак, правило: Чтобы получить уравнение «растянутой» в k раз по оси OZ поверхности S , нужно в уравнении исходной поверхности заменить z на .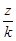

Рассмотрим теперь другие (не цилиндрические) часто встречающиеся поверхности 2го порядка.