JPEG-сжатие цифрового изображения
Одним из наиболее полных и популярных стандартов сжатия изображений является стандарт JPEG.
Сам процесс сжатия состоит из трех последовательных шагов:
а) Вычисление дискретного косинусного преобразования (ДКП) для матриц 8*8-блоков, полученных после стандартного разбиения матрицы ЦИ;
б) квантование коэффициентов ДКП;
в) кодирование неравномерным кодом.
Сначала ЦИ разбивается на отдельные блоки размером 8*8 элементов, которые обрабатываются последовательно слева направо и сверху вниз. Обработка каждого блока начинается со сдвига по яркости значений всех его 64 элементов, что достигается вычитанием величины 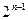 , где
, где 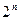 - максимальное число уровней яркости. Затем вычисляется двумерное ДКП элементов блока. Полученные значения коэффициентов квантуются в соответствии с формулой:
- максимальное число уровней яркости. Затем вычисляется двумерное ДКП элементов блока. Полученные значения коэффициентов квантуются в соответствии с формулой:
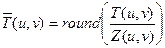 ,
,
где 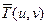 - результат квантования значения коэффициента ДКП
- результат квантования значения коэффициента ДКП 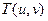 , а
, а 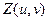 - соответствующий элемент матрицы коэффициентов квантования:
- соответствующий элемент матрицы коэффициентов квантования:
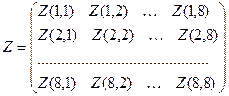 .
.
(Необходимо отметить, что перед тем, как квантованные коэффициенты ДКП 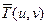 могут быть подвергнуты обратному ДКП для восстановления блока изображения, они должны быть умножены на
могут быть подвергнуты обратному ДКП для восстановления блока изображения, они должны быть умножены на 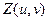 :
:
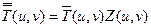 . (2.5)
. (2.5)
Очевидно, что обратное преобразование полученных значений 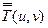 даст в результате приближение восстановливаемого блока изображения.)
даст в результате приближение восстановливаемого блока изображения.)
Отквантованные значения коэффициентов переупорядочиваются зигзаг-преобразованием согласно:
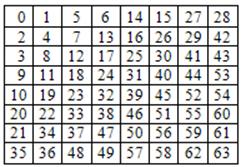
где показана очередность, в которой выбираются коэффициенты. Результатом является одномерная последовательность квантованных коэффициентов.
Одномерный массив, полученный после зигзаг-преобразования, упорядочивается по возрастанию пространственной частоты, при этом, как правило, возникают длинные последовательности нулей, что эффективно используется процедурой JPEG-кодирования. Рекомендованная JPEG матрица квантования имеет следующий вид:
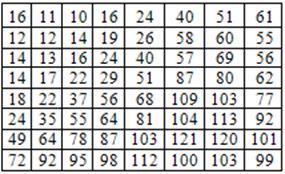
Пример. Последовательное кодирование и декодирование JPEG. Рассмотрим сжатие и восстановление следующего блока 8*8 элементов согласно стандарту последовательного кодирования JPEG:
Исходные пиксели могут иметь 256 или 28 уровней яркости, так что процесс кодирования начинается со сдвига диапазона значений – вычитания из значений пикселей величины 27 или 128. В результате получается массив:
который после прямого ДКП будет иметь вид:
Если для квантования полученных данных используется приведенная выше матрица квантования, то после квантования коэффициенты примут вид:
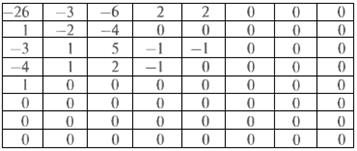
Процедура квантования дает значительное число нулевых элементов. После того, как коэффициенты переупорядочены в соответствии с зигзаг преобразованием, получится следующий массив:
(-26 -31 -3 -2 -6 2 -4 1 -4 1 1 5 0 2 0 0 -1 2 0 0 0 0 0 -1 -1 КБ)
Кодовое слово КБ означает конец блока, указывает на то, что все оставшиеся коэффициенты в переупорядоченной последовательности равны 0. Для кодирования полученного массива используются стандартные коды Хаффмана, преобразующие массив в непрерывный поток битов.
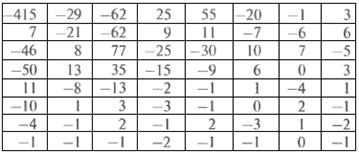
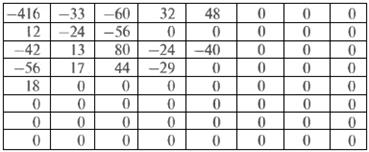
При восстановлении сжатого JPEG блока декодер в первую очередь должен из непрерывного потока битов воссоздать отквантованные коэффициенты ДКП. Поскольку последовательность двоичных кодов Хаффмана является однозначно декодируемой, этот шаг легко реализуется при помощи табличного преобразования. После умножения на коэффициенты квантования, согласно (2.5), получим массив:
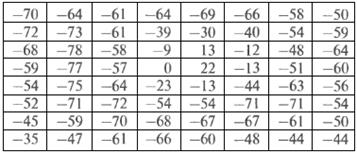
Полностью восстановленный блок получается после выполнения обратного ДКП полученного массива:
и обратного сдвига диапазона значений на +27=+128. В результате получаем:
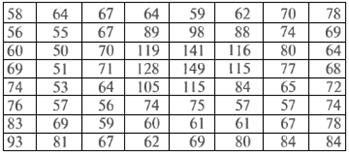
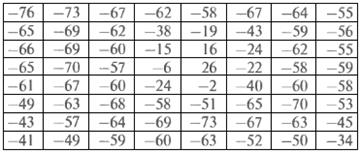
Все отличия значений элементов исходного и восстановленного блоков возникают вследствие самой природы сжатия с потерями, являющегося сутью JPEG процедур сжатия и восстановления. В данном примере ошибки восстановления находятся в диапазоне от -14 до 11 и распределены следующим образом:
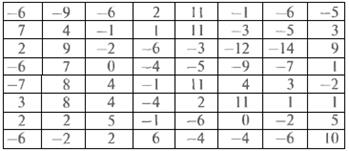
Характерные особенности сингулярных чисел блоков матрицы цифрового изображения при JPEG-сжатии.Пусть исходное ЦИ в градациях серого, хранящееся в некотором формате без потерь, например, в формате TIF, матрица которого 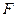 имеет размеры
имеет размеры 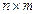 , разбивается стандартным образом на блоки
, разбивается стандартным образом на блоки 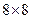 . Если для каждого блока
. Если для каждого блока 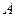 ЦИ определить множество всех СНЧ (сингулярный спектр), то оказывается, что в среднем лишь 2.40% от общего числа блоков (ОЧБ) имеют нулевые СНЧ.
ЦИ определить множество всех СНЧ (сингулярный спектр), то оказывается, что в среднем лишь 2.40% от общего числа блоков (ОЧБ) имеют нулевые СНЧ.
Данный факт не случаен. Ранг любой матрицы определяется количеством ее ненулевых СНЧ, а значит наличие нулей в сингулярном спектре будет говорить о том, что число ее линейно независимых строк (столбцов) меньше размера. Однако, для произвольного реального ЦИ, даже с учетом коррелированности значений яркости пикселей, вероятность того, что строки (столбцы) очередного блока окажутся линейно зависимыми, невелика.
Квантование коэффициентов DCT, которое происходит в процессе сохранения ЦИ в формате JPEG (с потерями), является необратимой процедурой и приводит к некоторым особенностям возмущений СНЧ блоков.
Пусть исходное ЦИ подверглось JPEG-сжатию. Проведем для него операцию частичного восстановления (ЧВ), которая включает в себя: 1) энтропийное декодирование; 2) умножение полученных коэффициентов на соответствующие элементы массива нормализации (матрицы квантования); 3) применение обратного DCT, но без последующего округления.
У полученной матрицы практически все блоки содержат нулевые СНЧ, причем таких значений в блоках будет достаточно много (табл.2.1). Такая ситуация закономерна. После квантования и округления коэффициентов DCT блоков многие из них, отвечающие высоким и средним частотам, обнулятся, оставаясь нулями после ЧВ, что, учитывая соответствие между коэффициентами дискретного преобразования Фурье и сингулярными тройками 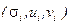 матрицы изображения, где
матрицы изображения, где 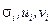 - СНЧ и отвечающие ему левый и правый СНВ соответственно, приведет к обнулению наименьших (а возможно и средних по величине) СНЧ матриц блоков.
- СНЧ и отвечающие ему левый и правый СНВ соответственно, приведет к обнулению наименьших (а возможно и средних по величине) СНЧ матриц блоков.
Табл.2.1. Результаты сингулярного разложения блоков  частично восстановленных изображений
частично восстановленных изображений
| Изображение в формате без потерь (TIF) | ОЧБ | Количества блоков, имеющих 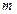 нулевых СНЧ нулевых СНЧ
| Кол-во блоков, у кот-х нулевых СНЧ больше 2-х, по отношению к ОЧБ (в %) | ||||||||
| m=8 | m=7 | m=6 | m=5 | m=4 | m=3 | m=2 | m=1 | m=0 | |||
| POUT | |||||||||||
| CAMERAMAN | |||||||||||
| TIRE | |||||||||||
| MOON | 99.8 | ||||||||||
| CELL |
Заметим, что, чем меньше нулевых СНЧ в рассматриваемом блоке, тем больше линий контура он содержит. Действительно, наличие контуров в блоке говорит о значительной высокочастотной составляющей в сигнале, отвечающем этому блоку. Тогда коэффициенты DCT, соответствующие высоким и средним частотам, будут сравнительно большими и могут остаться ненулевыми после квантования и ЧВ, а значит внесут свой вклад не только в максимальные СНЧ.
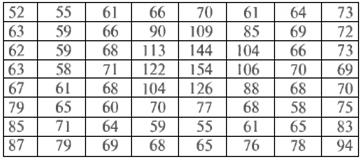
Для наглядного представления справедливости вышесказанного рассмотрим изображение СELL.TIF (рис.2.5(а)). На рис.2.5(б) представлена матрица нулевых СНЧ блоков (МНСЧБ) размерности 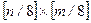 ЧВ-изображения, каждый элемент которой равен количеству нулевых СНЧ в соответствующем блоке. На рисунке выделены элементы, имеющие наименьшие значения, что позволяет наглядно увидеть соответствие между контурами исходного ЦИ и блоками, содержащими наименьшее количество нулевых СНЧ.
ЧВ-изображения, каждый элемент которой равен количеству нулевых СНЧ в соответствующем блоке. На рисунке выделены элементы, имеющие наименьшие значения, что позволяет наглядно увидеть соответствие между контурами исходного ЦИ и блоками, содержащими наименьшее количество нулевых СНЧ.
Пусть исходное изображение, подвергшееся JPEG-сжатию, восстанавливается полностью. Это означает, что после ЧВ все значения яркости пикселей округляются до целых и вводятся в диапазон 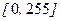 . Это действие возмутит матрицу изображения, полученную после ЧВ, определенным образом изменится количество нулевых СНЧ в блоках (табл.2.2). Там, где после ЧВ не было элементов, значительно меньших 0 или больших 255, возмущение матрицы будет небольшим. В соответствии с соотношением
. Это действие возмутит матрицу изображения, полученную после ЧВ, определенным образом изменится количество нулевых СНЧ в блоках (табл.2.2). Там, где после ЧВ не было элементов, значительно меньших 0 или больших 255, возмущение матрицы будет небольшим. В соответствии с соотношением
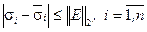 , (2.6)
, (2.6)
имеющим место для произвольной матрицы, где 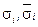 - СНЧ исходной и возмущенной матриц соответственно,
- СНЧ исходной и возмущенной матриц соответственно, 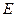 - матрица возмущений блока,
- матрица возмущений блока, 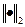 - спектральная матричная норма, СНЧ являются нечувствительными к возмущающим воздействиям. Если некоторые из нулевых СНЧ блоков матрицы ЧВ-изображения станут ненулями после полного восстановления (ПВ), то их значения будут сравнимы с погрешностью округления, что не характерно для блоков исходного ЦИ.
- спектральная матричная норма, СНЧ являются нечувствительными к возмущающим воздействиям. Если некоторые из нулевых СНЧ блоков матрицы ЧВ-изображения станут ненулями после полного восстановления (ПВ), то их значения будут сравнимы с погрешностью округления, что не характерно для блоков исходного ЦИ.
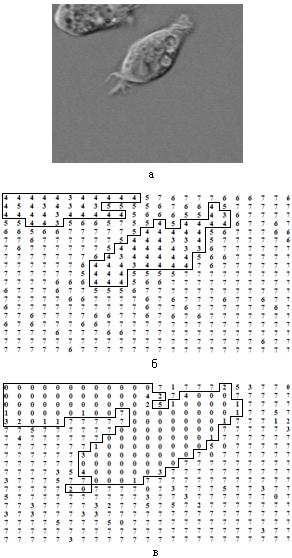
Рис.2.5. Исходное изображение СELL.TIF (а); МНСЧБ после ЧВ (б); МНСЧБ после полного восстановления (в)
Наиболее заметным различие между совокупным исходным изображением и полностью восстановленным после JPEG-сжатия будет при сравнении их МНСЧБ. Типичная картина представлена на рис.2.5(в), при этом МНСЧБ для CELL.TIF имела только нулевые значения.
Таблица 2.2. Результаты сингулярного разложения блоков полностью восстановленных изображений
| Изображение в формате без потерь (TIF) | ОЧБ | Количества блоков, имеющих 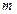 нулевых СНЧ нулевых СНЧ
| Кол-во блоков, у которых нулевых СЧ больше двух, по отношению к ОЧБ (%) | ||||||||
| m=8 | m=7 | m=6 | m=5 | m=4 | m=3 | m=2 | m=1 | m=0 | |||
| POUT | |||||||||||
| CAMERAMAN | |||||||||||
| TIRE | |||||||||||
| MOON | |||||||||||
| CELL |
Вопросы
- Что означает сжатие даннях? Что такое избыточность даннях?
- Основные виды избыточности данных.
- Как реализуется сжатие посредством квантования?
- Что такое малоранговая оппроксимация изображения? Как реализуется сжатие посредством использования малоранговых аппроксимаций изображения?
- Что такое сингулярное разложение матрицы?
- Что такое спектральное разложение матрицы?
- Соответствие между параметрами цифрового изображения в пространственной и частотной областях.
- Основные шаги JPEG-сжатие цифрового изображения. Матрицы квантования.
- Характерные особенности сингулярных чисел блоков матрицы цифрового изображения при JPEG-сжатии.
- Частичное и полное восстановление цифрового изображения после сжатия.
Литература
- Кобозева А.А. Анализ информационной безопасности / А.А.Кобозева, В.А.Хорошко. – К.: Изд. ГУИКТ, 2009. – 251 с.
- Деммель Дж. Вычислительная линейная алгебра / Дж.Деммель; пер.с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 430 с.
- Бахвалов Н.С. Численные методы / Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. — М.: БИНОМ. Лаборатория знаний, 2006. — 636 с.
- Гонсалес Р. Цифровая обработка изображений / Р.Гонсалес, Р.Вудс; пер. с англ. под ред. П.А.Чочиа. — М.: Техносфера, 2005. — 1072 с.
- Каханер Д. Численные методы и программное обеспечение / Д.Каханер, К.Моулер, С.Нэш; пер. с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 575 с.
- Гантмахер Ф.Р. Теория матриц / Ф.Р.Гантмахер. — М.: Наука, 1988. — 552 с.
- Воеводин В.В. Вычислительные основы линейной алгебры / В.В.Воеводин. — М.: Наука. Гл.ред.физ.-мат.лит., 1977. — 304 с.
Дата добавления: 2015-09-18; просмотров: 1881;
