Достаточные условия изображения.
Теорема. Если 1)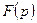 
голоморфна в полуплоскости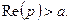 
2) 
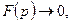если 
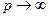в полуплоскости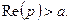
3) 
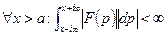- интегрировать на любой вертикальной прямой.
То: а) функция 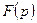является изображением некоторой функции-оригинала 
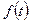с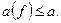 
б) справедлива формула обращения Меллина: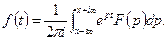 
Доказательство. 1)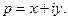 
Определим функцию 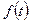интегралом Меллина при некотором 
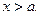Проверим, что интеграл сходится: 
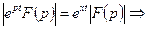интеграл сходится по признаку сравнения. Более того, он сходится равномерно по t на компактах вещественной оси: 
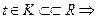функция 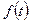- непрерывна.
|
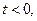то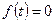 
по лемме Жордана, применённой к полуплоскости 
( 
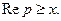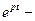убывает при 
).
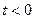3) Заметим, что функция 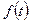не зависит от 
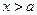по ИТК.
Интеграл по контуру прямоугольника = 0.
Интегралы по основаниям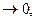 
т.к. функция стремится к 0.
Значит интегралы по вертикальным прямым равны 0.
4) Оценим: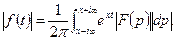 
В этом интеграле – всё есть некоторые константы, кроме 
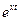(т.к. сходится к const). 
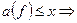(можем так подобрать)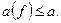
|
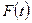является изображением этой функции: Зафиксируем р0: 
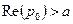и будем вычислять интеграл Лапласа: 
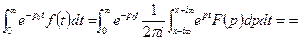В этой формуле х будем брать любым, большим а. Возьмём 
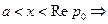абсолютно сходится двойной интеграл 
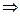можем изменить порядок интегрирования (по теореме Фубини), тогда 
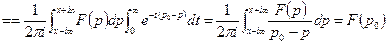по теореме Коши о вычетах.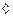 
Пояснения к последнему равенству (как применять теорему Коши): Интеграл по замкнутому
Контуру равен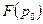 
, но когда распрямляем и 
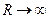, то интеграл 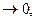по дуге
Окружности.
Дата добавления: 2015-09-02; просмотров: 894;