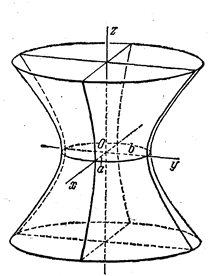
Однополостный гиперболоид.

Если вращать гиперболу 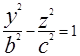вокруг оси OZ, то в результате получим поверхность 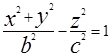(1), она называется однополостным гиперболоидом вращения. Растянем этот гиперболоид по оси ОХ в к раз тогда х заменим на 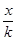. Обозначим 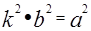. В результате получим каноническое уравнение однополостного гиперболоида общего вида. 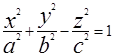(2). 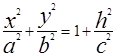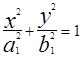Если рассекать однополостный гиперболоид плоскостями параллельными плоскости XOY, их уравнение z=h, то в сечении получим эллипсы: или (3), где 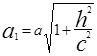, 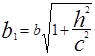. Самый малый эллипс будет с полуосями a и b при z=0 : 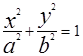- так называемый горловой эллипс. 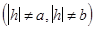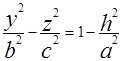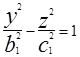При сечении плоскостями x=h и y=h получаем гиперболы , или (4) 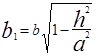, 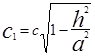. 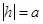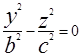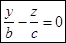В частности при уравнение (4) имеет вид или и 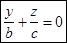- уравнения прямых. Значит, на однополостном гиперболоиде лежат прямые линии.

Из сказанного ясно, что однополосный гиперболоид имеет вид бесконечной трубки бесконечно расширяющиеся в обе стороны от горлового эллипса. Он состоит из одного куска, одной полости. Он имеет три плоскости симметрии - координатные плоскости.