Гиперболический параболоид.
Это поверхность второго порядка, которая определяется уравнением 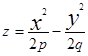 (1). Гиперболический параболоид уже не может быть получен методом вращения и растяжения, не относится он и к числу цилиндров. Чтобы представить вид поверхности выясним вопрос о сечениях. При пересечении плоскостью Z=h получаются гиперболы
(1). Гиперболический параболоид уже не может быть получен методом вращения и растяжения, не относится он и к числу цилиндров. Чтобы представить вид поверхности выясним вопрос о сечениях. При пересечении плоскостью Z=h получаются гиперболы 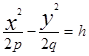 (2) или
(2) или 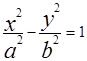 . (3) , где
. (3) , где 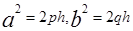 ; в сечении плоскостями Х=h , Y=h получим параболы
; в сечении плоскостями Х=h , Y=h получим параболы 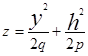 и
и 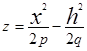 . В окрестности начала координат гиперболический параболоид имеет вид седла .
. В окрестности начала координат гиперболический параболоид имеет вид седла .

Замечание:
Хотя гиперболический параболоид имеет сложную форму , эта поверхность является линейчатой, то есть может быть составлена из одних прямых также как цилиндры, конусы и однополосный гиперболоид. Эту особенность этих поверхностей используют в строительстве. Русский инженер Шухов предложил конструкции из металлических балок, расположенных также как расположены прямолинейные образующие однополосного гиперболоида (вращения). Такие конструкции оказались легкими и прочными. Они часто употребляются для устройства высоких радиомачт, водонапорных башен.
 |
II.Введение в математический анализ.
Дифференциальное исчисление функций одной переменной
План
1.Число. Переменная. Функция.
§1. Величина и число. 72
§2. Абсолютная величина действительного числа и её свойства. 73
§3. Переменные и постоянные величины. 74
§4. Область изменения переменной величины. 75
§5. Понятие функции. 76
§6. Способы задания функции. 77
§7. Обратная функция и её график. 79
§8. Понятие сложной функции. 81
§9. Основные характеристики поведения функции. 81
§10. Элементарные функции. 82
§11. Некоторые приёмы построения графиков функций. 88
2. Предел. Непрерывность.
§1. Упорядоченная переменная величина. 90
§2. Предел переменной величины. 90
§3. Предел функции. 92
§4. Бесконечные пределы функции. Бесконечно большие величины. 93
§5. Ограниченные функции. 95
§6. Бесконечно малые величины (б. М. В.) и их основные свойства. 95
§7. Основные теоремы о действиях над пределами. 97
§8. Неопределённые выражения. 99
§9. Другие свойства пределов. 100
 §10. Предел функции sin x/x при x 0. 101
§10. Предел функции sin x/x при x 0. 101
§11. Число е. 102
§12. Понятие о гиперболических функциях. 103
§13. Натуральные логарифмы. 105
§14. Сравнение бесконечно малых величин. 105
§15. Эквивалентные бесконечно малые величины. 106
§16. Непрерывность функции в точке и на промежутке. 108
§17. Точки разрыва функции. 110
§18. Действия над непрерывными функциями. 111
§19. Свойства функций, непрерывных на сегменте. 113
3. Дифференциальное исчисление.
§1. Задачи, приводящие к понятию производной функции. 116
§2. Определение производной функции. 118
§3. Уравнение касательной и нормали к графику функции. 120
§4. Связь между непрерывностью и дифференцируемостью функции. 121
§5. Производные постоянной, синуса, косинуса и степенной функции. 121
§6. Производные суммы, произведения и частного. 122
§7. Производные обратной и сложной функций. 123
§8. Производные обратных тригонометрических функций. 124
§9. Производные логарифмической и показательной функций. 125
§10. Производные степенной и степенно-показательной функций. 125
§11. Производные гиперболических функций. 126
§12. Таблица основных формул дифференцирования. 126
§13. Неявная фнукция и её дифференцирование. 127
§14. Параметрически заданные функции и ихз дифференцирование. 128
§15. Дифференциал функции. 129
§16. Дифференциалы основных элементарных функций, суммы,
произведения и частного. 131
§17. Инвариантность формы дифференциала функции. Дифференциал
сложной функции. 132
§18. Производные высших порядков. 133
§19. Дифференциалы высших порядков. 135
§20. Производные высших порядков от функций, заданных
неявно и параметрически. 136
4. Свойства дифференцируемых функций
и некоторые применения производных.
§1. Теоремы о «средних» значениях функции. 137
§2. Применение производной к нахождению пределов функций.
Правило Лопиталя. 142
§3. Формула Тейлора. 145
5. Исследование функций с помощью производных.
Построение графиков функций.
§1. Условия постоянства, возрастания и убывания функций. 148
§2. Экстремумы функций. 149
§3. Наибольшее и наименьшее значение функции на отрезке. 155
§4. Направление вогнутости кривой и точки перегиба. 157
§5. Асимптоты кривой (графика функции). 160
§6. Полное исследование функции и построение её графика. 164
6. Кривизна кривой.
§1. Длина дуги кривой. Дифференциал длины дуги. 167
§2. Кривизна плоской кривой. Её вычисление. 171
§3. Радиус, круг и центр кривизны. Понятие эволюты и эвольвенты. 173
I.ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ.
§1. Величина и число.
При исследовании явлений природы и в своей практической деятельности человек сталкивается с множеством различных величин. Например:
время, скорость, вес, сила, масса - это физические величины; атомный вес, коэффициент растворимости - химические величины; объём, площадь, длина - геометрические и т.д.
Величин чрезвычайно много, но все они обладают одним характерным свойством - каждая величина может быть измерена величиной того же рода, принятой за единицу измерения.
Так, для температуры единицей измерения является 10, длины – 1м, и т.п. Результатом всякого измерения является отвлеченное число, которое выражается отношением рассматриваемой величины к её единице измерения.
Это отвлеченное число называется числовым значением или просто значением данной величины.
ЭТО НУЖНО РАЗЛИЧАТЬ:
сама величина, являясь отображением определенного качества предмета, всегда конкретна (длина, вес), значение же величины - отвлеченное число.
Число может быть целым (если единица содержится целое число раз в измеряемой величине), дробным (если существует другая единица, которая содержится целое число раз как в измеряемой величине, так и в прежней единице) и иррациональным (когда такой общей единицы не существует, т.е. данная величина оказывается несоизмеримой с единицей измерения).
Вам известно, что диагональ квадрата несоизмерима с его стороной. Поэтому, если сторона квадрата = 1, то длина диагонали будет выражаться числом Ö2. Оно является иррациональным. Иррациональным является и число p, равное длине полуокружности диаметром 1. Примерами иррациональных чисел могут служить Ö3, Ö5, 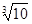 , и т.п.
, и т.п.
Из арифметики известно, что всякое рациональное число может быть представлено в виде конечной десятичной дроби или бесконечной периодической десятичной дроби. И обратно: всякая конечная или бесконечная периодическая десятичная дробь выражает рациональное число: 3/5=0,6; 1/6=0,1666666...=0,1(6).
Всякое же иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби и наоборот: всякая бесконечная непериодическая десятичная дробь есть иррациональное число. Например, число p=3,141592…
Все рациональные и иррациональные числа вместе образуют множество действительных или вещественных чисел. Каждое вещественное число может быть геометрически изображено в виде точки на числовой оси, т.е. на прямой, на которой выбрано начало отчета, соответствующее числу ноль и отмечена точка соответствующая числу 1. Вправо от нуля откладываются положительные числа, влево - отрицательные.

рис. 1
Строго доказано, что каждому действительному числу соответствует единственная точка на оси и наоборот, каждой точке оси соответствует единственное действительное число. Поэтому обычно выражение «число х» и «точка y» считают равнозначными. Важными свойствами множества действительных чисел являются следующие:
1. Между любыми двумя действительными числами x и y (x¹y) есть сколько угодно как рациональных, так и иррациональных чисел;
2. Всегда выполняется одно из соотношений: x=y или x<y или Х>У. Большему числу соответствует точка на числовой оси, лежащая правее.
§2. АБСЛЮТНАЯ ВЕЛИЧИНА ДЕЙСТВИТЕЛЬНОГО ЧИСЛА И ЕЁ СВОЙСТВА
Определение.
Абсолютной величиной (модулем) некоторого действительного числа x называют само это число x, если оно неотрицательное (x³0) или число - x, если x - отрицательное.
 Принято обозначать |Х|. Согласно определению
Принято обозначать |Х|. Согласно определению
, если x³0,
, если x<0.
Геометрически модуль числа x означает расстояние, на которое удалена на числовой прямой точка x от начала координат.
 |
|3|=3; |-2|=2; |0|=0.
Из определения абсолютной величины следует выполнение для " действительных x неравенства х£|x|.
Рассмотрим некоторые свойства.
1. Абсолютная величина суммы двух или нескольких чисел не больше суммы абсолютных величин отдельных слагаемых:
|х1+х2+...+хn|£|х1|+|х2|+...+|хn|.
Доказательство.
Докажем для двух слагаемых, для большего числа аналогично.
|х1+х2|£|х1|+|х2|
1.)х1+х2³0. Тогда |х1+х2|=х1+х2£|х1|+|х2|;
2.) х1+х2<0, тогда |х1+х2|=-(х1+х2)=(-х1)+(-х2)£|х1|+|х2|;
других возможностей быть не может, доказано полностью.
Примеры:
|(-2)+3|<|-2|+|3|=5, 1<5
2. Абсолютная величина разности не меньше разности абсолютных величин, т.е. |x-y|³|x|-|y|.
Доказательство.
Положим x-y=z. Тогда x=z+y. По доказанному |x|=|z+y|£|z|+|y| или |z|³|x|-|y| или |x-y|³|x|-|y|;
3. Абсолютная величина произведения нескольких сомножителей равна произведению абсолютных величин этих сомножителей.
|х1×х2×…×хn|=|х1|×…×|хn|
Доказательство.
следует из самого определения действия умножения:
x1×x2×…×xn=±|x1|×|x2|×…×|xn|=>|x1×x2×…×xn|=|±|x1|×|x2|×…×|xn|=|x1|×|x2|×…×|xn|.
Следствие:
|хn|=|х|n, |хn|=|х×х×¼×х|=|х|×|х|×¼×|х|=|х|n
n раз n раз
4. Абсолютная величина частного двух чисел равна частному от деления абсолютных величин делимого и делителя 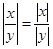 .
.
Доказательство.
Обозначим x/y=z, тогда x=y×z, |x|=|y×z|=|y|×|z|Þ|z|=|x|/|y| или 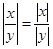 .
.
5. Неравенство |x|<d для d>0, равносильно -d<x<d, неравенство |x|>d равносильно двум x>d и x<-d.
§3. ПЕРЕМЕННЫЕ И ПОСТОЯННЫЕ ВЕЛИЧИНЫ.
В конкретных науках (физике, химии и т.п.) часто нужно знать с какой именно величиной имеют дело, т.е. учитывают качественную характеристику величины (вес, скорость и т.п.). В математике отвлекаются от качественных свойств и говорят о некоторой абстрактной величине, обозначая ее символически буквами x, y и т.д. И имеют дело лишь с числовыми значениями этой величины. Это обстоятельство позволяет выводы математики применять к исследованию самых разных конкретных величин.
В математике различают два вида величин: постоянные и переменные.
Определение:
Величина называется постоянной, если она всегда (или хотя бы в условиях данной задачи) сохраняет одно и то же числовое значение.
Примеры.
Сумма углов треугольника, скорость света в вакууме, абсолютный ноль -273 градуса.
Определение.
Величина называется переменной, если она в условиях даже одной задачи принимает различные числовые значения.
Примеры.
Температура воздуха в течение дня, скорость движения машины, расстояние от Солнца до Земли,…
Бывает порой так, что одна и та же величина в одних условиях может считаться постоянной, в других переменной. Так ускорение силы тяжести в пределах Земли может меняться, но в конкретном месте постоянно. Иногда величина кажется постоянной, но она переменная. Например, ход часов зависит от температуры, тряски и т.п.
Величины, которые сохраняют постоянное значение в любых условиях, называются абсолютными постоянными (сумма углов треугольника, число p и др.).
Высшая математика изучает преимущественно переменные величины и их взаимосвязь между собой.
§4. ОБЛАСТЬ ИЗМЕНЕНИЯ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ.
Переменная величина принимает разные числовые значения в зависимости от ее характера и условий задачи. Так температура воды принимает значения от 0 до 100 градусов 0£t£1000, -¥£tga£+¥, -1£sinx£1,…. Часто числовые значения переменной величины обозначаются той же буквой x.
Определение.
Совокупность всех числовых значений переменной величины x называют областью изменения этой переменной.
Наиболее часто встречаются следующие области изменения переменной величины, называемые обычно промежутками:
Интервал (а,b)- множество всех чисел x, удовлетворяющих неравенству
a<x<b
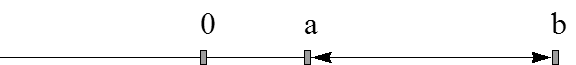
а и b - концы интервала, а - левый, b - правый.
Сегмент - (замкнутый интервал) [a, b] - множество всех чисел x, удовлетворяющих неравенству a£x£b
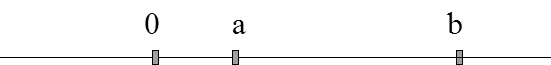
а и b - концы, a-b - длина сегмента.
Полусегмент [a, b): из всех a£x<b, полуинтервал (a, b]: a<x£b

Рассматривают и бесконечные промежутки: (-¥,¥) - из всех чисел, вся прямая; (-¥,a) - из всех чисел x<a; (a,+¥) - из всех чисел x>a, [a,+¥) и т.п.
 Окрестность точки а - множество всех действительных чисел x, удовлетворяющих неравенству a-d<x<a+d; (d>0), т.е. интервал длины 2d с центром в точке а.
Окрестность точки а - множество всех действительных чисел x, удовлетворяющих неравенству a-d<x<a+d; (d>0), т.е. интервал длины 2d с центром в точке а.
d называется часто радиусом окрестности, а саму окрестность называют d - окрестностью.
То, что число x принадлежит некоторому промежутку, обозначается значком Î.
xÎ(a,b).
Например: 2Î[0,5]

§5. ПОНЯТИЕ ФУНКЦИИ.
В природе, при решении практических и технических задач, а потому и в математике, приходиться учитывать взаимосвязь величин. Так пройденный путь при равномерном движении зависит от времени: S=v·t, площадь круга зависит от его радиуса Р=pR2. Одна переменная тут (t,R) является независимой, принимает произвольные допустимые значения (0£t<+¥, 0£R<+¥), другая (s,Р) является зависимой или функцией, она принимает уже соответствующие значения. Область изменения их уже [0,+¥).
Дадим строгое определение функции для произвольных величин.
Пусть x и y две переменные величины, имеющие соответственно области изменения Х и У.
Определение:
Переменная величина y называется функцией от переменной величины x в области её изменения Х, если по некоторому правилу или закону каждому значению x из X ставиться в соответствие одно определенное значение y из У.
Записывается: y=f(x), y=φ(x) и т.п.
При этом х называется независимым переменным или аргументом функции.
Множество Х называется областью определения или существования функции, множество Y - областью изменения функции. Символ f, φ называется характеристикой функции и указывает на закон соответствия.
Область определения X функции либо указывается либо находится по самой функции.
Например:
y=х2, Х=(-¥,+¥), т.к. x может принимать любые значения. Y=[0,+¥), т.к. y=х2³0 при любом x.
Задав некоторое значение аргумента х=х0, мы можем вычислить соответствующее значение функции y0=f(х0).
Например:
х0=2, у0=22=4.
Функцию у=f(x) можно изобразить графически на плоскости.
Определение:
Графиком функции у=f(х), определенной в некоторой области Х, называют множество всех точек М(х,у) плоскости, координаты которых связаны соотношением у=f(х).
В этом смысле само равенство у=f(х) называется уравнением этого графика. Обычно график функции это некоторая кривая.
 Замечание:
Замечание:
 Мы говорим только об однозначной функции, т.е. когда каждому x соответствует одно y.
Мы говорим только об однозначной функции, т.е. когда каждому x соответствует одно y.



 Если одному x соответствует два и более y, то функция называется многозначной. Мы рассматриваем однозначные, если это не оговаривается.
Если одному x соответствует два и более y, то функция называется многозначной. Мы рассматриваем однозначные, если это не оговаривается.
§6. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ.
Задать функцию, значит указать область ее определения Х и правило f, при помощи которого по данному значению аргумента xÎX находится соответствующее ему значение функции.
Важнейшими способами задания функции являются: табличный, аналитический, графический, с помощью программы.
I. Табличный способ.
При этом способе в определенном порядке выписываются значения аргумента и соответствующие значения функции.
| x | х1 | х2 | х3 | х4 | х5 | х6 | х7 |
| y | у1 | у2 | у3 | у4 | у5 | у6 | у7 |
Таковы, например, таблицы логарифмов, тригонометрические, таблицы квадратов и т.д.
Особенно распространен в естествознании и технике. Результаты эксперимента обычно записываются в виде таблицы.
Например: давление зависит от температуры.
| Давление | Р1 | Р2 | Р3 |
| Температура | t1 | t2 | t3 |
Удобство в том, что по значению аргумента сразу без вычислений видно значение функции.
Недостатками являются: 1.) Нельзя вписать в таблицу все значения аргумента, поэтому для промежуточных значений аргумента вычисления производить нужно, результаты приблизительные, 2.) Не очень наглядно виден характер изменения функции, особенно если таблица большая.
II.Аналитический способ (задание формулой).
Формулой или аналитическим выражением называют символическое обозначение совокупности известных математических операций, которые производятся в определенной последовательности над числами и буквами, обозначающими постоянные и переменные величины.
Например:
x2+lgx, 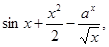 и т.п.
и т.п.
Если функциональная зависимость y=f(х) такова, что f обозначает формулу (аналитическое выражение), то говорят, что функция задана аналитически.
Так у=sinх, 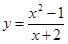 , S=pR2 и т.п. - функция задана аналитически.
, S=pR2 и т.п. - функция задана аналитически.
Иногда при аналитическом задании употребляют сразу несколько формул.
y=|x| и 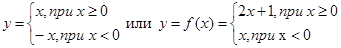
Область определения функции при этом способе часто не указывается. Тогда за область определения принимают, так называемую, естественную область определения функции, т.е. совокупность всех тех значений аргумента, при которых функция не теряет числового смысла.
Так, 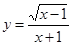 . Естественная область определения х+1¹0, x¹-1, x-1³0, x³1, т.е. X: x³1 X=[1,+¥).
. Естественная область определения х+1¹0, x¹-1, x-1³0, x³1, т.е. X: x³1 X=[1,+¥).
Естественную область определения называют еще областью существования функции.
В ряде случаев область существования может не совпадать с областью определения.
Так, если 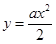 - скорость равноускоренного движения без начальной скорости. Исходя из формулы, -¥<x<¥ - любое. Но время х не может быть меньше нуля: 0£x<¥. Область определения - часть области существования.
- скорость равноускоренного движения без начальной скорости. Исходя из формулы, -¥<x<¥ - любое. Но время х не может быть меньше нуля: 0£x<¥. Область определения - часть области существования.
Аналитический способ - основной в математическом анализе.
Выгоды - компактность, возможность вычислить функции для любого значения аргумента из области определения и возможность применять методы анализа. Недостаток - отсутствие наглядности и необходимость производить вычисления, часто громоздкие.
III. Графический способ.
Если на плоскости имеется линия, которая пересекается прямыми, параллельными оси OY лишь в одной точке, то каждому х соответствует единственное y, т.е. линия определяет функцию у=f(x).Сама линия называется графиком этой функции.
Графическое задание функции особенно распространено в физике и технике.
Так все самопишущие приборы в виде кривых (графиков) задают зависимость величин: кардиограф - колебания сердца, термограф - колебания температуры и т.п.
 |
Достоинство - наглядность, быстрое нахождение значений функции. Недостаток - неточность вычисления значения функции.
§7. ОБРАТНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК.
Пусть имеется функция у=f(x), Х - ее область определения, Y - область значений. Мы знаем, что каждому х0ÎC соответствует единственное значение у0=f(х0), у0ÎY.
Может оказаться, что каждому уÎU (или ее части U1) соответствует тоже единственное х из Х.

Тогда говорят, что на области U (или ее части U1) определена функция x=j(y) обратная для функции у=f(x).
Например:
1) у=х3. X=(-¥,¥) Y=(-¥,¥), обратная функция 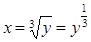 , область определения Y=(-¥,¥), область значений X=(-¥,¥)
, область определения Y=(-¥,¥), область значений X=(-¥,¥)
2) y=x2.
 X=(-¥,¥); Y=[0,¥)
X=(-¥,¥); Y=[0,¥)
x=± 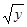 – однозначной обратной функции нет: каждому y соответствуют два значения x. Если же рассмотреть y=x2 с областью определения X1=[0,¥); Y=[0,¥), то ей существует обратная x=+√y область определения Y=[0,¥), область изменения X=[0,¥).
– однозначной обратной функции нет: каждому y соответствуют два значения x. Если же рассмотреть y=x2 с областью определения X1=[0,¥); Y=[0,¥), то ей существует обратная x=+√y область определения Y=[0,¥), область изменения X=[0,¥).
Графики прямой и обратной функции совпадают, очевидно. Но принято обычно аргумент обозначать через х, а функцию через у. Поэтому обратные функции записались бы так: y= 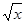 , y=±
, y=± 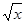 . Графики этих функций остались такими же линиями, если бы переобозначить оси координат. Но это тоже не делают, ось ОХ всегда горизонтальна. Поэтому график обратной функции можно получить либо по точкам, либо отобразив его зеркально относительно биссектрисы 1 и 3-го квадрантов, т.к. переобозначение координат на точки биссектрисы не влияет.
. Графики этих функций остались такими же линиями, если бы переобозначить оси координат. Но это тоже не делают, ось ОХ всегда горизонтальна. Поэтому график обратной функции можно получить либо по точкам, либо отобразив его зеркально относительно биссектрисы 1 и 3-го квадрантов, т.к. переобозначение координат на точки биссектрисы не влияет.

§8. ПОНЯТИЕ СЛОЖНОЙ ФУНКЦИИ (ФУНКЦИИ ОТ ФУНКЦИИ).
Пусть переменная y есть функция от переменной u: y=F(u), а переменная u есть сама функция от переменной x u=j(x). Тогда y тоже зависит от x. Пусть функция u=j(x) определена на X и область её значений U, функция y=F(u) определена либо на всей U (либо на её части U, 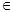 U). Тогда каждому xÎX соответствует единственное uÎU, а этому u соответствует единственное yÎY. Тем самым на X определена функция
U). Тогда каждому xÎX соответствует единственное uÎU, а этому u соответствует единственное yÎY. Тем самым на X определена функция 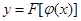 - которая называется сложной функцией или функцией от функции. При этом x – независимая переменная (аргумент), u – промежуточная переменная, y - функция.
- которая называется сложной функцией или функцией от функции. При этом x – независимая переменная (аргумент), u – промежуточная переменная, y - функция.
Пример:
у=sinх2 - это сложная функция: у=sinu, u=х2.
Сложная функция может образовываться и более чем из двух звеньев. Так 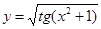 . Тут у=Öu, u=tgv, v=х2+1.
. Тут у=Öu, u=tgv, v=х2+1.
Задание сложной функции называется еще цепным заданием.
§9. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ПОВЕДЕНИЯ ФУНКЦИИ.
Для изучения функции у=f(x) бывает полезно исследовать ее на четность, на периодичность, на монотонность. Дадим соответствующие определения, будем полагать, что значения аргумента x изменяются, возрастая и принимая все промежуточные значения.
Дата добавления: 2015-10-05; просмотров: 1424;
