Эллипсоид

Будем вращать эллипс 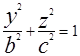вокруг оси OZ. Получим поверхность 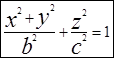(1) , которая называется эллипсоидом вращения. Если растянуть эллипсоид по оси OX в к раз, то в уравнение (1) координаты х заменятся на 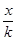и мы получим 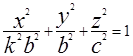. Положив 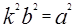мы получим каноническое уравнение эллипсоида общего вида. 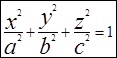.(2)

Если рассекать эллипсоид какой либо плоскостью, параллельной одной из координатных плоскостей, то получим эллипс.

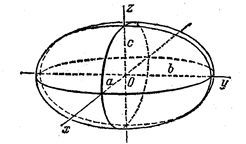Например, пологая z=h, -c<h<c, получим в сечении эллипс 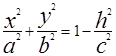или, если разделить обе части на 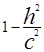и положить 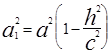, , 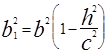то получим 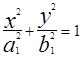. Аналогично, пологая x=h или y=h, получим тоже эллипсы. Этим и объясняется название поверхности - эллипсоид. Числа a,b,c называются полуосями эллипсоида. Если они различны, то эллипс называют трёхосным. Эллипс (1) будет двуосным. Сфера, очевидно, есть частный случай эллипсоида, когда a=b=c=R.

Замечание. Первоначальный эллипс можно вращать и около оси OY. Получим тоже эллипсоид. Он называется вытянутым, а от вращения около оси OZ - сжатым.