Эллиптический параболоид.
Если вращать параболу 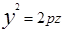 (р>o), вокруг оси oz, то в результате получим поверхность называемую параболоидом вращения. Его уравнение
(р>o), вокруг оси oz, то в результате получим поверхность называемую параболоидом вращения. Его уравнение 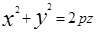 или
или 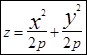 (1). Если растянуть этот параболоид по оси OY в к раз, то получим параболоид общего вида - эллиптический параболоид. Его уравнение
(1). Если растянуть этот параболоид по оси OY в к раз, то получим параболоид общего вида - эллиптический параболоид. Его уравнение 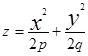 (2), здесь
(2), здесь 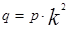 , т.к. Y заменится на
, т.к. Y заменится на 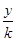 , числа р и q > 0, очевидно. В сечении параболоида (2) плоскостями z=h>0 получим эллипсы
, числа р и q > 0, очевидно. В сечении параболоида (2) плоскостями z=h>0 получим эллипсы 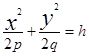 или
или 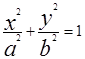 , где
, где 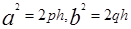 .С ростом h полуоси эллипсов бесконечно увеличиваются. В сечении плоскостями x=h и y=h получаются параболы
.С ростом h полуоси эллипсов бесконечно увеличиваются. В сечении плоскостями x=h и y=h получаются параболы 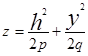 и
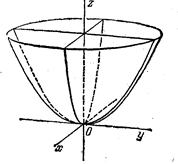
и 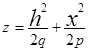 . Параболоид (2) расположен над плоскостью XOY и касается ее в началe координат. О(0,0,0).
. Параболоид (2) расположен над плоскостью XOY и касается ее в началe координат. О(0,0,0).
|
Дата добавления: 2015-10-05; просмотров: 742;
