Определение 1.
Функция у=f(x) называется четной, если при изменении знака y любого значения аргумента, значение функции не изменится f(-x)=f(x). Функция называется нечетной, если при изменении знака у любого значения аргумента изменяется только знак значения функции, а абсолютная величина значения остается прежней f(-x)=-f(x).
Заметим, что функция полагается определенной на симметричном относительно начала координат промежутке.
Например, у=х2, у=cosx - четные, у=х3, у=sinх - нечетные.
 |
Графики четных функции симметричны относительно оси OY, нечетных - симметричны относительно начала координат. Ясно, что бывают функции ни четные, ни нечетные: (у=2x).
Определение 2.
Функция у=f(х) называется периодической, если существует такое положительное число l, что для любого x справедливо равенство f(x+l)=f(x) (1).
Если функция периодическая, то верны и равенства f(x+2l)=f(x), f(x-3l)=f(x) и вообще f(x+kl)=f(x) (к - любое целое число). Наименьшее число l, при котором выполняется равенство (1), называется периодом функции у=f(x).
Например.
у=sinx, y=cosx имеют период l=2p, y=tgx, y=ctgx имеет l=p.
График периодической функции повторяется, поэтому достаточно вычертить его в промежутке длиной в 1 период l.
Определение 3.
Функция называется возрастающей в некотором интервале, если любому большему значению аргумента соответствует большее значение функции. Функция называется убывающей на интервале, если любому большему значению аргумента соответствует меньшее значение функции.
Таким образом, если х1, х2 любые значения из (а, b) и а£х1<х2£b, то f(x1)<f(x2) - в случае возрастающей функции и f(x1)>f(x2) - в случае убывающей.
Так у=2х возрастает, а  - убывает в (-¥,¥). Интервал (а,b) называется интервалом возрастания или убывания функции или интервалом монотонности.
- убывает в (-¥,¥). Интервал (а,b) называется интервалом возрастания или убывания функции или интервалом монотонности.
§10. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ.
Среди большого числа различных функций в математическом анализе особо выделяют класс элементарных функций. Это класс функций, которые конструируются из простейших элементарных (или основных элементарных), а также постоянных с помощью конечного числа операций сложения, вычитания, умножения, деления, возведения в степень, извлечения корней и взятия 
функций от функций. Элементарные функции задаются аналитически.
К основным элементарным функциям относятся:
1) Степенная функция: у=хa (a-действительное число);
2) Показательная функция: у=ах (а¹1, а>0 - действительное число).
3) Логарифмическая функция: у=logах, где основание а>0, а¹1 - действительное число.
4) Тригонометрические функция: у=sinx, y=cosx, y=tgx, y=ctgx, иногда у=secx=1/cosx, y=cosecx=1/sinx.
5) Обратные тригонометрические функции: y=arcsinx, y=arccosx , y=arctgx, y=arcctgx, y=arcsecx, y=arccosecx.
Рассмотрим области определения и графики основных элементарных функций.
1) Степенная у=xa.
1. a=n - натуральное число, у=хn - парабола, X=(-¥,¥);
2. a=-n - целое отрицательное, у=х-n, X=(-¥,0)+(0,-¥) - гипербола;
в) a=m/n- дробное положительное, у=хm/n=n 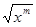 - область определения и график зависит от четности и нечетности m и n.
- область определения и график зависит от четности и нечетности m и n.
Так a=2/3, y=3Öх2, C=(-¥,¥) у>0;
a=3/2, y=Öх3, C=[0,+¥), y>0;
a=3/5, y=5ÖХ3, C=(-¥,¥), y-любое.
2.Логарифмическая функция
у=logах, C=(0,¥), a>0, a¹1
а>1 - возрастает,
а<1 - убывает,
 3.Показательная функция
3.Показательная функция
 |
у=ах, C=(-¥,¥), а>1- возрастает, а<1- убывает,
4.Тригонометрические
у=sinx, y=cosx, C=(-¥,¥),
y=tgx, x¹p/2+kp

y=ctgx, x¹kp;
 |
5.Обратные тригонометрические
y=arcsinx, х=[1,1], y=arccos x ,х=[-1,1], y=arctgx,х=(-¥,¥), y=arcctgx.

Примерами элементарных функций могут служить  и т.д.
и т.д.
Важными примерами элементарных функций являются:
1.) Целая рациональная или многочлен:
у=а0хn+а1хn-1+...+аn(a0,a1,…,an - любые д.ч., коэффициенты, n-степень). Область определения: C=(-¥,¥).
Частными случаями являются:
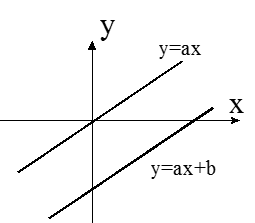
1) у=ах+b - линейная функция. /При b=0, у=ах – прямая пропорциональная зависимость у от x. При а=0, у=b - постоянная. График есть прямая || OX/. Можно построить у=ах (проходит через начало) и поднять или опустить на b по оси ординат.
2) у=ах2+вх+с - квадратичная функция. Определена для любого х. График есть парабола. При а>0 ветви направлены вверх, при а<0 - вниз. Если уравнение у=ах2+вх+с=0 имеет два действительных корня х1 и х2, то парабола пересекает ось OX в точках х=х1 и х=х2, если корни действительны и равны, то касается оси OX в точке х=х1=х2. Если корни мнимые, то не пересекает ось OX, расположена выше или ниже оси OX.

2.) Дробно-рациональная.
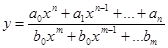 - отношение двух многочленов.
- отношение двух многочленов.
Частным случаем является дробно-линейная 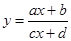 , (а,b,с,d - числа, с - не равно нулю). Область определения все х¹-d/c. Если а=0, d=0, то имеем
, (а,b,с,d - числа, с - не равно нулю). Область определения все х¹-d/c. Если а=0, d=0, то имеем 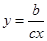 - обратная пропорциональная зависимость, график - гипербола с осями в качестве асимптот. В общем случае графиком дробно-линейной функции является тоже гипербола, асимптотами которой являются прямые х=-d/с, и у=а/с.
- обратная пропорциональная зависимость, график - гипербола с осями в качестве асимптот. В общем случае графиком дробно-линейной функции является тоже гипербола, асимптотами которой являются прямые х=-d/с, и у=а/с.
 Например:
Например:
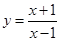 , а=1, b=1, с=1, d=-1,
, а=1, b=1, с=1, d=-1,
х=-d/с=1, у=1.
Есть и другие виды элементарных функций. Например, иррациональные (содержат аргумент под корнем).
Рациональные и иррациональные образуют множество алгебраических функций. Элементарные функции, не являющиеся алгебраическими, называются трансцендентными: у=sinx, y=ах, и т.п.
§11. НЕКОТОРЫЕ ПРИЕМЫ ПОСТРОЕНИЯ ГРАФИКОВ ФУНКЦИЙ.
График функции можно построить, исследовав данную функцию, выяснив особенности хода ее графика. Но в ряде случаев график функции можно построить, исходя из графиков основных элементарных функций. При этом полезны следующие правила:
1. График функции у=f(x+а) получается из графика функции у=f(x), если перенести ось ординат параллельно самой себе на а единиц (вправо, при а>0, влево при а<0).
Например: у=2х+3
Каждая точка графика у=f(х+а) получается при абсциссе на а единиц меньшей, чем такая же точка у графика у=f(х). А это и достигается перемещением оси ординат.

2. График функции y=f(х)+b получается из графика y=f(х) переносом оси абсцисс параллельно себе на b единиц (вверх при b<0, вниз при b>0).
Доказательство.
Любая ордината графика у=f(х)+b на b единицу «увеличена», чем у графика y=f(x). Но это «увеличение» и достигается смещением оси OX.
3. График функции у=k×f(х) получается из графика у=f(х) «растяжением» его по вертикали в k раз, например: у=(2/3)2х, при к>1 - действительное растяжение, при к<1 - сжатие.

4.График функции у=f(k×х) получается из графика функции у=f(х) «сжатием» графика у=f(х) по горизонтали в k раз, при этом точка графика с абсциссой х=0 остается неизменной, при k>1 - сжатие, при k<1 - растяжение.
Например, у=22/3х, строим y=2x, сжимаем его к оси OY в 2/3 раза.
 При построении более сложных графиков эти правила применяются в совокупности. При этом сначала производят сжатие по оси абсцисс, затем перенос оси ординат, сжатие по оси ординат, и перенос оси абсцисс.
При построении более сложных графиков эти правила применяются в совокупности. При этом сначала производят сжатие по оси абсцисс, затем перенос оси ординат, сжатие по оси ординат, и перенос оси абсцисс.
Например:
у=2×22(х-1)+1, строим y=2x; сжимаем график к оси OY в 2 раза, получаем y=22x; переносим ось OY на 1 влево, получаем y=22(x-1); растягиваем его от оси OX в 2 раза, получаем y=2×22(x-1); ось OX опускаем вниз на 1. Полученный график в этой системе и будет искомым.

II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ.
§1.УПОРЯДОЧЕННАЯ ПЕРЕМЕННАЯ ВЕЛИЧИНА.
Пусть имеется некоторая переменная величина х. Она принимает определенные числовые значения из своей области изменения. Если про каждые из двух значений переменной можно сказать, какое является предыдущим, а какое последующим, то переменная называется упорядоченной.
Например, частным случаем упорядоченной переменной величины является такая, значения которой можно снабдить номерами и записать в порядке следования номеров в виде числовой последовательности: {xn}={х1, х2, х3,...,хn,...}. Ясно, что за значением хк следует значение хк+1, а предшествует хк-1 независимо от их величины.
Определение 1.
Упорядоченная переменная величина называется возрастающей (убывающей), если каждое последующее ее значение больше (меньше) предыдущего. Возрастающие и убывающие переменные величины называются вместе монотонно изменяющимися или монотонными величинами.
Определение 2.
Переменная величина х называется ограниченной, если есть такое число К>0, что все последующие значения ее, начиная с некоторого, удовлетворяют равенству -K£x£K или все равно |x|£K.
 |
Иначе, величина х ограничена, если, начиная с некоторого все последующие значения ее расположены на [-K,K] (но вовсе не обязательно заполняют сегмент весь).
§2. ПРЕДЕЛ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ.
Пусть х - упорядоченная переменная величина (например числовая последовательность).
Определение.
Постоянное число a называют пределом переменной величины х, если какое бы сколь угодно малое положительное число e мы не взяли, можно указать такое значение переменной х, что все последующие значения переменной будут удовлетворять неравенству |x-а|<e.
Символически это пишут х®а или limх=а (от латинского limes - предел).
 |
Геометрически это определение означает, что какую бы малую e - окрестность точки a мы не взяли, все последующие значения x после некоторого будут лежать в этой окрестности.
Из чертежа видно, что неравенство 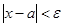 означает, что расстояние от точки х до а меньше e. А это и есть внутренность окрестности. Точка х удовлетворяет, очевидно, и двойному неравенству a-e<x<a+e. Так что неравенства
означает, что расстояние от точки х до а меньше e. А это и есть внутренность окрестности. Точка х удовлетворяет, очевидно, и двойному неравенству a-e<x<a+e. Так что неравенства 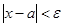 и это равнозначны.
и это равнозначны.
 |
Определение: Для числовой последовательности {xn} a является пределом, если по
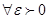 можно указать такой номер N, что для всех
можно указать такой номер N, что для всех 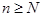
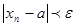
Для членов последовательности все значения xN,xN+1 и далее лежат внутри  -окрестности обязательно.
-окрестности обязательно.
Переменную x, значения которой образуют числовую последовательность x1,x2,…,xn часто записывают в виде члена последовательности x=xn или {xn}. Например, {1/n}. Это переменная величина или последовательность с общим членом xn=1/n: 1,1/2,1/3…
Пример: Пусть переменная величина x принимает последовательно значения: x1=2/1, x2=3/2, x3=4/3, …,xn=(n+1)/n,… т.е. образуют числовую последовательность. Докажем, что 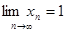 .
.
Возьмём 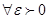 .
. 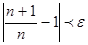
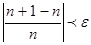
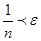 . Как только номер n станет
. Как только номер n станет 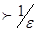 , его примем за N. Тогда неравенство будет выполняться для
, его примем за N. Тогда неравенство будет выполняться для 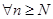 . Но тогда всё доказано.
. Но тогда всё доказано.
Теорема 1: предел постоянной величины равен этой постоянной. Доказательство: Постоянная величина является частным случаем переменной – все её значения =с: x=c/ Но, тогда limc=c. 
Теорема 2: Переменная величина x не может иметь двух пределов.
Доказательство: Допустим limx=a и limx=b. Тогда 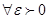
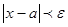
и 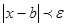 после некоторого значения x. Но тогда
после некоторого значения x. Но тогда
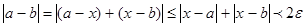 . Так как
. Так как  сколь угодно мало, то неравенство возможно лишь при a=b
сколь угодно мало, то неравенство возможно лишь при a=b
Замечаеие: Переменная может и не иметь предела: x=xn=(-1)n=-1,+1,-1,+1. Расстояние до любой точки а от её значений –1,+1 не может быть меньше 1/2 
 (-1)n не имеет предела.
(-1)n не имеет предела.
Мы предполагали а – числом. Но переменная x может стремиться и к бесконечности.
Определение: Переменная x стремится к бесконечности, если для 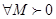 начиная с некоторого значения x вес остальные значения удовлетворяют неравенству
начиная с некоторого значения x вес остальные значения удовлетворяют неравенству 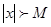 . Переменная x стремится к
. Переменная x стремится к 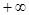 , если при тех же условиях выполняется неравенство x>M и к -
, если при тех же условиях выполняется неравенство x>M и к -  , если при тех же условиях выполняется неравенство x<-M. Если переменная X стремится к бесконечности , то её называют бесконечно большой величиной и пишут
, если при тех же условиях выполняется неравенство x<-M. Если переменная X стремится к бесконечности , то её называют бесконечно большой величиной и пишут 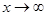
Пример: x=xn=n2. Возьмём 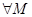 >0. Должно выполняться n2>M. n>
>0. Должно выполняться n2>M. n> 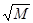 . Как только n удовлетворяет этому неравенству, так для всех xn=n2 неравенство выполняется. Значит, n2
. Как только n удовлетворяет этому неравенству, так для всех xn=n2 неравенство выполняется. Значит, n2 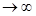 , а точнее n2
, а точнее n2 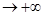 .
.
§3. ПРЕДЕЛ ФУНКЦИИ. 
Будем предполагать, что аргумент х функции у=f(х) стремится к х0 или ¥.
Рассмотрим поведение функции y в этих случаях.
Определение.
Пусть функция у=f(х) определена в некоторой окрестности точки х0. Число A называется пределом функции при х®х0, если для любого e>0, сколь угодно малого, можно указать такое число d>0, что для всех х¹х0 и удовлетворяющих неравенству |x-x0|<d выполняется неравенство |f(х)-A|<e.
Если A есть предел функции f(х), то пишут  или f(х)®А при х®х0.
или f(х)®А при х®х0.
 Определение так можно проиллюстрировать геометрически.
Определение так можно проиллюстрировать геометрически.
Если А есть предел f(х) при х®х0, то взяв любую e- окрестность точки А, мы всегда можем указать такую d - окрестность точки х0, что для всех х из этой d - окрестности значения функции f(х) отстоят от А не дальше e, т.е. попадут в выбранную e- окрестность точки А, или, все равно, часть графика соответствующая точкам х из d- окрестности лежит целиком в полосе шириной 2e.
Видно, что чем меньше e, тем меньше должно быть и d.
Определение.
Пусть аргумент х стремится к точке х0, принимая все время значения x>x0 (x<x0).Тогда число А1(А2), к которому стремится функция f(х), называется пределом функции f(х) в точке х0 справа (слева) или правосторонним (левосторонним).
Записывается: limх®х0+0f(х)=А1 , (limх®х0-0f(х)=А2).
Можно доказать, что если предел limх®х0f(х)=А существует, то существуют в этой точке и оба односторонних предела и они равны, А1=А2=А. Обратно: Если существуют односторонние пределы и они равны, то существует и общий предел. Если же хоть один не существует или они не равны, то предел функции не существует.
Пример.
Доказать, что f(х)=3х-2 имеет предел при х®1 равный 1.
Любое e>0, d-?, |х-1|<d Þ |3х-2-1|<e, |3х-3|<e, 3|х-1|<e, |х-1|<e/3.
В качестве d можно взять любые положительные числа £e/3; 0<d£e/3.
Доказали, что для любого e>0 достаточно взять d£e/3, чтобы из 0<|х-1|<d Þ|f(х)-1|<e, но это и значит, что limX®1(3х-2)=1.
Определение.
 Число А называется пределом функции у=f(х) при х®¥, если для любого e>0 (сколь угодно малого) можно указать такое положительное число P, что для всех значений х, удовлетворяющих неравенству |х|>P выполняется неравенство |f(х)-А|<e.
Число А называется пределом функции у=f(х) при х®¥, если для любого e>0 (сколь угодно малого) можно указать такое положительное число P, что для всех значений х, удовлетворяющих неравенству |х|>P выполняется неравенство |f(х)-А|<e.
Записывают limх®¥f(х)=А.
Геометрически это означает, что для любого e график функции для х>p и х<-p располагается в полосе шириной 2e.
Пример.
f(х)=1/х при х®¥, f(х)®0.
Какое бы e>0 ни взяли, график функции при х>Р и х<-Р расположится в полосе шириной 2e.
|1/х|<e, 1/х<e, х>1/e, Р=1/e.
Аналогично определяются и 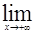 f(х)=А1 и
f(х)=А1 и 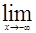 f(х)=А2. В первом случае должно выполняться неравенство |f(х)-А1|<e для х>Р, во втором |f(х)-А2|<e при х<-Р (Р>0).
f(х)=А2. В первом случае должно выполняться неравенство |f(х)-А1|<e для х>Р, во втором |f(х)-А2|<e при х<-Р (Р>0).
Так, 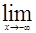 1/х=0, и
1/х=0, и 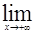 1/х=0. Равенство их и позволяет рассматривать общий предел
1/х=0. Равенство их и позволяет рассматривать общий предел  1/х=0.
1/х=0.
§4. БЕСКОНЕЧНЫЕ ПРЕДЕЛЫ ФУНКЦИИ.
БЕСКОНЕЧНО БОЛЬШИЕ ВЕЛИЧИНЫ.
До сих пор мы считали, что А – это некоторое число. Полезно обобщить понятие предела на тот случай, когда функция неограниченно возрастает по абсолютной величине.
Определение.
Функция f(х) при х®х0 имеет пределом ¥ (стремиться к бесконечности), если для любого наперед заданного числа М>0 (сколь угодно большого) можно найти d>0, что для всех х¹х0 и удовлетворяет неравенству |х-х0|<d выполняется неравенство |f(х)|>M.
Символически записывается так:  f(х)=¥ или f(х)®¥ при х®х0.
f(х)=¥ или f(х)®¥ при х®х0.
Если f(х)®¥ при х®х0 и принимает только положительные или только отрицательные значения, то соответственно пишут  f(х)=+¥ или
f(х)=+¥ или  f(х)=-¥.
f(х)=-¥.
При этом определение дословно аналогичное, только должно выполняться неравенство f(х)>M, или f(х)<-M.
Геометрически это означает, что каким бы большим ни было число М>0, найдется d- окрестность точки х0, для всех точек которой график функции расположен выше прямой у= М и ниже у=-М.

Пример
у=1/х2, при х®0 у=f(х)®+¥. Возьмем любое М>0, должно выполняться 1/х2>М, х2<1/М, |х|<1/ÖМ, d=1/ÖМ. Например М=4, d=1/2.
Нетрудно дать и определение ¥ предела функции при х®¥.  f(х)=¥: если для любого М>0 можно указать Р>0, что из |х|>RÞ |f(х)|>M.
f(х)=¥: если для любого М>0 можно указать Р>0, что из |х|>RÞ |f(х)|>M.
Самим дать определение 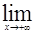 f(х)=¥,
f(х)=¥, 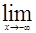 f(х)=¥,
f(х)=¥, 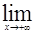 f(х)=-¥ и т.п.
f(х)=-¥ и т.п.
Определение.
Функция f(х) называется бесконечно большой величиной (б.б.в.) при х®х0 или х®¥, если она стремится к бесконечности.
Так, 1/х2- бесконечно большая величина при х®0. Следует не смешивать понятия б.б.в. и очень большого числа . Б.б.в.- это переменная величина.
Замечание:
Функция у=f(х) при х®х0 или х®¥ может не иметь ни конечного ни бесконечного предела.
Например: у=sin 1/х, при х®0 она не имеет предела;
у=cosх, при х®¥ - не имеет предела.

§5.ОГРАНИЧЕННЫЕ ФУНКЦИИ
Функция у=f(х) называется ограниченной в некоторой области определения Х, если существует такое число К>0, что для любого хÎХ выполняется неравенство |f(х)|£К. Если такого К не существует, то функция называется неограниченной в Х.
Очевидно б.б.в. при х®х0 являются неограниченными в окрестности точки х0. Справедлива теорема.
Теорема.
Если существует конечный предел  f(х)=А, то в некоторой окрестности точки х0 функция у=f(х)- ограничена.
f(х)=А, то в некоторой окрестности точки х0 функция у=f(х)- ограничена.
Доказательство.
Пусть e>0 любое число, тогда найдется d>0, что для любого хÎ(х0-d,х0+d), |f(х)-А|<e или |f(х)|-|A|£| f(х)-А|<e Þ |f(х)|< |A|+e, (|A|+e=К). Это и означает ограниченность f(х) в (х0-d,х0+d) .
Обратная теорема неверна. Так функция у=sin1/х ограничена в окрестности 0, но предела при х®0 не имеет.
§6.БЕСКОНЕЧНО МАЛЫЕ ВЕЛИЧИНЫ (Б.М.В.) И ИХ ОСНОВНЫЕ СВОЙСТВА
Определение. Функция, имеющая пределом 0 при х®х0 (x®¥) называется бесконечно малой величиной, или просто бесконечно малой при х®х0 (x®¥).
Обычно б.м.в. обозначают символами a(х), b(х),g(х) и т.д.
Из определения следует, что a(х)есть б.м.в. при х®x0, если для любого e>0 найдется d>0 такое ,что для|х-х0|<dÞ |a(х)|<e.
Пример:
функция a(х)=х2 есть б.м.в. при х®0, т.к 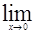 х2=0.
х2=0.
функция a(х)=sinх есть б.м.в. при х®0, х®p¼; a(х)=logах при х®1 и т.п.
Замечание.
Не следует смешивать б.м.в. и очень малое число. Только число 0 считается б.м.в. так как  0=0. В дальнейшем говорим о пределах при х®х0 ,хотя все верно и для х®¥.
0=0. В дальнейшем говорим о пределах при х®х0 ,хотя все верно и для х®¥.
Теорема 1 .
Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
Доказательство.
Пусть a1(х),a2(х),...an(х)- б.м.в. при х®х0.
Докажем ,что a(х)= a1(х)+...+ an(х)- б.м.в.
Возьмем любое e>0. Найдем d1, что для |х-x0|<d1 |a1(х)|<e/n;
Найдем d2 что для |х-x0|<di , |a2(х)|<e/n;
Найдем dn , что для |х-x0|<dn |an(х)|<e/n;
Возьмем d=min{d1,¼,dn}.
Тогда для этого любого e>0 при d>0 из |х-x0|<dÞ одновременное выполнение всех неравенств.
Но тогда |a(х)|=|a1(х)+¼+an(х)|£|a1(х)|+¼+|an(х)|<e/n+...+e/n=n×e/n=e, т.е. |a(x)|<e что и требовалось доказать.
Замечание: для случая бесконечного числа б.м.в. теорема может быть не верна. Например:
 a(х)=1/х+...+1/х (х-раз.), 1/х- есть б.м.в. при х®¥, а a(х)=1, и®1¹0, т.е. не является б.м.
a(х)=1/х+...+1/х (х-раз.), 1/х- есть б.м.в. при х®¥, а a(х)=1, и®1¹0, т.е. не является б.м.
Теорема 2.
Произведение б.м.в. a(х) при х®х0 или х®¥ на функцию, ограниченную в окрестности точки х0 (¥) есть величина б.м.
Доказательство. Пусть a(х) б.м.в. при х®х0 и в некоторой окрестности {х0-d1, х0+d1} функция f(х) ограничена, т.е. |f(х)|<K для всех х из этой окрестности. Но так как  a(х)=0 , то для любого e>0 найдется d2>0, что для х: |х-х0|<d2, т.е. для xÎ{х0-d2, х0+d2} выполняется |f(х)|<e/К. Выберем d=min{d1,d2}тогда для х, удовлетворяющего неравенству |х-х0|<d, выполняются оба неравенства, и потому |a(х)×f(х)|<K×e/K=e. Но это и значит, что a(х)×f(х)- б.м.в. при х®х0.
a(х)=0 , то для любого e>0 найдется d2>0, что для х: |х-х0|<d2, т.е. для xÎ{х0-d2, х0+d2} выполняется |f(х)|<e/К. Выберем d=min{d1,d2}тогда для х, удовлетворяющего неравенству |х-х0|<d, выполняются оба неравенства, и потому |a(х)×f(х)|<K×e/K=e. Но это и значит, что a(х)×f(х)- б.м.в. при х®х0.
Следствие 1. Произведение б.м.в. на постоянную есть б.м.в.(при х®х0).
Следствие 2. Произведение б.м.в. на величину, имеющую предел, есть б.м.в. (при х®х0).
Следствие 3.Произведенеие нескольких б.м.в. есть б.м.в. (при х®х0).
Следствие 4.Целая положительная степень б.м.в. есть б.м.в.
Теорема 3.( о связи б.м.в. и б.б.в.)
Если величина a(х) б.м. при х®х0 (и не обращается в нуль), то обратная ей величина 1/a(х) есть б.б.в.
Доказательство.
Возьмем любое М>0 и считаем e=1/М. Тогда т.к. a(х)®0 при х®х0, то для e=1/М>0 найдется d>0, что для çх-х0ê<d выполняется неравенство ça(х)ê<1/М, или для тех же çх-х0ê<d. ç1/a(х)ê>М, что и означает, что 1/a(х)®¥ при х®х0, т.е. 1/a(х) б.б.в.
Верно и обратное: если f(х) – б.б.в. при х®х0 и f(х) не обращается в 0, то 1/f(х) – б.м.в. при х®х0.
Т.к. f(х) б.б.в., то для любого e>0 найдется d>0, что для çх-х0ç<d çf(х)ç>1/e Þç1/f(х)ç< 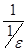 <e для тех же х, ч.т.д.
<e для тех же х, ч.т.д.
Например. х2®0 при х®0. 1/х2®¥ при х®0.
Теорема 4. (о связи предела и б.м.в.)
Функцию у=f(х), имеющую пределом число А при х®х0 или х®¥, можно представить в виде суммы этого числа и некоторой б.м.в.: f(x)=А+a(х).
Обратно, если функцию у=f(х) можно представить в виде суммы некоторого числа А и некоторой бесконечно малой a(х), то А есть предел функции:  f(x)=А.
f(x)=А.
Доказательство.
1) Пусть limC®C0 f(x)=А. Это значит, что для любого e>0 найдется d>0 , что для х:|х-х0|<d будет |f(x)-А|<e. Обозначим f(x)-А=a(х), тогда |a(х)|<e, а это означает что a(х) б.м.в. Откуда f(x)=А+a(х) и a(х)®0 при х®х0.
2) Наоборот.
Пусть f(x)=А+a(х) и a(х)®0 при х®х0. Тогда для любого e>0 найдется d>0, что из |х-х0|<d следует |a(х)|<e или |f(x)-A|<e. А это и означает, что  f(x)=А.
f(x)=А.
§7.Основные теоремы о действиях над пределами
Будем по-прежнему говорить о х®х0, хотя все верно и для х®¥.
Теорема 1.
Предел алгебраической суммы нескольких функций, имеющих конечные пределы, равен алгебраической сумме пределов этих функций:
 (f1(x)±f2(x)±...±fn(x))=
(f1(x)±f2(x)±...±fn(x))=  f1(x)±...±
f1(x)±...±  fn(x).
fn(x).
Доказательство.
Приведем для 2–х. Пусть  f1(x)=А1,
f1(x)=А1,  f2(x)=А2. Тогда по теореме 4 f1(x)=А1+a1(х) и f2(x)=А2+a2(х)-a1(х) и a2(х)- б.м.в. при х®х0.
f2(x)=А2. Тогда по теореме 4 f1(x)=А1+a1(х) и f2(x)=А2+a2(х)-a1(х) и a2(х)- б.м.в. при х®х0.
Но тогда f1(x)±f2(x)=А1±А2+a1(х)±a2(х) отсюда 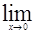 (f1(x)±f2(x))= = А1±А2 =
(f1(x)±f2(x))= = А1±А2 =  f1(x)±
f1(x)±  f2(x).
f2(x).
Пример.

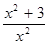 =
=  (1+
(1+ 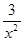 )=
)=  1 +
1 + 
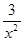 =1+0=1.
=1+0=1.
Теорема 2.
Предел произведения нескольких функций, имеющих конечные пределы, равен произведению пределов этих функций:
 (f1(x)×f2(x)×...×fn(x))=
(f1(x)×f2(x)×...×fn(x))=  f1(x)×...×
f1(x)×...×  fn(x).
fn(x).
Доказательство. (для 2-ух).
Пусть  f1(x)=А1,
f1(x)=А1,  f2(x)=А2. Тогда по теореме 4 f1(x)=А1+a1(х) и f2(x)=А2+a2(х).
f2(x)=А2. Тогда по теореме 4 f1(x)=А1+a1(х) и f2(x)=А2+a2(х).
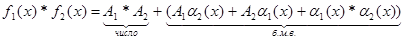 . По теореме 4
. По теореме 4
 f1(x)*f2(x)=А1*А2 ч.т.д.
f1(x)*f2(x)=А1*А2 ч.т.д.
Следствие. Постоянный множитель можно выносить за знак предела  С*f(x)=С*
С*f(x)=С*  f(x)
f(x)
Доказательство.
 С = С. По теореме 2 все сразу следует.
С = С. По теореме 2 все сразу следует.
Пример.
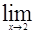 3х2 = 3
3х2 = 3 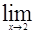 х2= 3*22=3*4=12.
х2= 3*22=3*4=12.
Теорема 3.
Предел частного двух функций, имеющих конечные пределы, равен частному их пределов, если предел знаменателя не равен нулю:  f1(x)/f2(x)=
f1(x)/f2(x)=  f1(x)/
f1(x)/  f2(x).
f2(x).
Доказательство.
Пусть  f1(x)=А1,
f1(x)=А1,  f2(x)=А2¹0. Тогда f1(x)=А1+a1(x), f2(x)=А2+a2(х).
f2(x)=А2¹0. Тогда f1(x)=А1+a1(x), f2(x)=А2+a2(х).
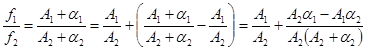
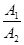 - число, а второе слагаемое б.м.в., т.к. в знаменателе стоит величина, имеющая пределом А22. Но тогда
- число, а второе слагаемое б.м.в., т.к. в знаменателе стоит величина, имеющая пределом А22. Но тогда 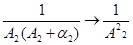 - конечное число. Произведение б.м.в. в числителе на величину, имеющую предел, есть б.м.в. Но тогда
- конечное число. Произведение б.м.в. в числителе на величину, имеющую предел, есть б.м.в. Но тогда  .
.
Замечание.
Т.к. числовая последовательность {xn} может считаться функцией от натурального аргумента n
хn = f(n):x1 = f(1), x2 = f(2), то все теоремы о пределах функций верны и для числовых последовательностей. Пир этом n®¥, и только:
1) lim(xn±yn)=lim xn ± lim yn
2) lim(xnyn)=lim xn  lim yn
lim yn
3) lim(xn/yn)=lim xn/lim yn
lim c*xn=c lim xn
Пример.
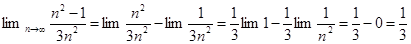
§8.Неопределенные выражения
В рассмотренных теоремах о пределах речь шла о существовании конечных пределов слагаемых, сомножителей, числителей и знаменателей( причем знаменатель не равен нулю).
В случае несоблюдения этих требований, теоремы уже неприменимы, и сказать сразу о существовании предела и тем более его величине для таких выражений нельзя. Такие выражения называют неопределенными (или неопределенностями). Исходя из теорем можно сделать вывод о существовании четырех видов неопределенностей:
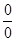 ,
, 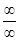 , 0×¥, ¥-¥.
, 0×¥, ¥-¥.
1) 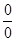 - это неопределенность
- это неопределенность 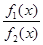 , когда f1(х)®0 и f2(х)®0
, когда f1(х)®0 и f2(х)®0
при х®х0. 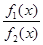 может быть б.м.в., б.б.в., иметь предел ¹0 или вообще не иметь никакого предела.
может быть б.м.в., б.б.в., иметь предел ¹0 или вообще не иметь никакого предела.
Например, 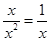 , при х®0 это б.б.в.,
, при х®0 это б.б.в., 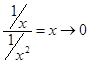 б.м.в., и т.п.
б.м.в., и т.п.
2) 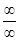 - это неопределенность
- это неопределенность 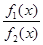 , когда f1(х)®¥ и f2(х)®¥, для
, когда f1(х)®¥ и f2(х)®¥, для 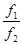 может быть любой из четырех случаев.
может быть любой из четырех случаев.
3) 0×¥ - это неопределенность f1(х)×f2(х), когда f1(х)®0, а f2(х)®¥. Для f1(х)×f2(х) может быть тоже четыре вида.
4) ¥-¥ - это неопределенность f1(х)- f2(х), когда f1(х)®+¥, f2(х)®+¥. Для f1(х)- f2(х) может быть четыре вида.
Т.к. теоремы о пределах в этих случаях неприменимы, то исходя из конкретного вида переменных в каждом отдельном примере, проводят преобразования, позволяющие найти предел. (Эти преобразования называются раскрытием неопределенности).
Примеры: 1.) 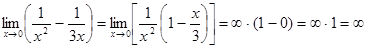
1.) 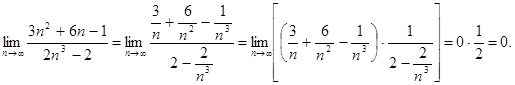
§9. ДРУГИЕ СВОЙСТВА ПРЕДЕЛОВ.
Теорема 4. (О пределе промежуточной функции). Если значения функции f(x) заключены между соответствующими значениями функций u(x) и v(x): u(x)£f(x)£v(x), и при этом u(x) и v(x) при x®x0 (или x®¥) стремятся к одному и тому же пределу А, то f(x) стремится к этому же пределу А при x®x0 (x®¥).
Доказательство. Пусть x®x0 и u£f£v, u®А и v®А. Это значит, что для "e>0 найдется d1>0, что "x:|x-x0|< d1=>|u(x)-A|<e или
A-e<f(x)<A+e (1)
найдется d2>0, что "x|x-x0|<d2=>|v(x)-A|<e или A-e<v(x)<A+e (2)
Возьмем d=min{d1,d2}, (тогда для "х:|x-x0|<d) (1) и (2) выполняется одновременно и, значит, и неравенство
А-e<u(x)£f(x)£v(x)<A+e или A-e<f(x)<A+e или |f(x)-A|<e. Последнее показывает, что  . ч.т.д.
. ч.т.д.
Теорема 5. Если при х®х0(или х®¥) функция f(x) принимает неотрицательные значения f(x)³0 и при этом стремится к пределу А, то А есть число неотрицательное А³0. Если f(x)£0, то А£0.
 Доказательство. Пусть f(x)®A при x®x0 и f(x³0). Допустим, что А<0, тогда |f(x)-A|³|A|>0. Откуда следовало бы, что при x®x0 f(x)®A, что противоречит условию теоремы. Противоречие доказывает, что должно быть А³0. Аналогично доказывается и второе утверждение.
Доказательство. Пусть f(x)®A при x®x0 и f(x³0). Допустим, что А<0, тогда |f(x)-A|³|A|>0. Откуда следовало бы, что при x®x0 f(x)®A, что противоречит условию теоремы. Противоречие доказывает, что должно быть А³0. Аналогично доказывается и второе утверждение.
Теорема 6. Если для функций u(x) и v(x), имеющих пределы при x®x0 (или при x®¥), выполняется соотношение u(x)£v(x), то имеет место 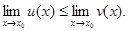
Доказательство. По условию u(x)£v(x)=>u(x)-v(x)£0. По т. 5 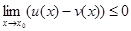 или
или 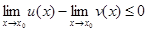 .
.
Теорема 4 позволяет, не находя предела сказать, существует ли предел функции f(x), если ограничивающие её функции имеют одинаковые пределы. Такого типа теоремы называются теоремами существования. Приведем важный признак существования предела монотонной числовой последовательности (т.е. возрастающей или убывающей). Будем говорить, что последовательность х1,х2,…,хn,… ограничена сверху, если найдется такое число K, что для всех n хn£K; будем говорить, что последовательность ограничена снизу, если найдется такое k, что для всех n k£xn. Последовательность, ограниченную и снизу и сверху называют просто ограниченной: k£xn£K. Числовая последовательность называется возрастающей, если для любого n
xn-1<xn, убывающей, если для любого n xn-1>xn.
Теорема. (без док-ва).
Если числовая последовательность х1,х2,…,хn,… возрастающая и ограничена сверху, то она имеет предел. Если числовая последовательность х1,х2,…,хn,… убывающая и ограничена снизу, то она имеет предел.
Если последовательность ограничена сверху числом К, то хn£К, но возрастая, они стремятся к некоторому числу А (об этом и говорит теорема). Ясно, что А£К. Если последовательность возрастающая и неограниченная сверху, то хn®+¥. Убывающая и ограниченная снизу хn®a³k, неограниченная хn®-¥.
Одной ограниченности числовой последовательности мало, чтобы она имела предел.
Например: хn=(-1)n: -1,1,-1,1…, не имеет предела, хотя и ограниченная. Она не является монотонной. Такие не монотонные называются иногда колеблющимися последовательностями. Колеблющаяся последовательность, даже ограниченная, может не иметь предела.
§10. Предел функции  при х®0 (х – радианная мера угла).
при х®0 (х – радианная мера угла).
Теорема.
Функция  при х®0 имеет предел равный 1:
при х®0 имеет предел равный 1: 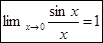 (1)
(1)
Предел (1) называется первым замечательным пределом.
Доказательство.
Функция f(х)=  определена в окрестности точки х=0, а в самой точке нет. Имеем неопределенность
определена в окрестности точки х=0, а в самой точке нет. Имеем неопределенность 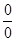 . Для нахождения предела рассуждаем следующим образом.
. Для нахождения предела рассуждаем следующим образом.
 Рассмотрим окружность радиуса 1 и в ней центральный угол х, причем, 0<х<p/2. Построим хорду АВ и касательную в точке А (линию тангенсов). Видим, что SDABО<SсектВОА<SDОСА или учитывая, что SDABО=
Рассмотрим окружность радиуса 1 и в ней центральный угол х, причем, 0<х<p/2. Построим хорду АВ и касательную в точке А (линию тангенсов). Видим, что SDABО<SсектВОА<SDОСА или учитывая, что SDABО= 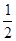 АО×ОВ×sinх=
АО×ОВ×sinх= 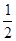 ×1×1×sinх; SсектВОА=
×1×1×sinх; SсектВОА= 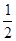 ОА×ÈАВ=
ОА×ÈАВ= 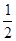 ×1×х=
×1×х= 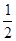 х; SDОАС=
х; SDОАС= 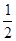 ОА×СА=
ОА×СА= 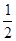 ×1×tgх=
×1×tgх= 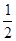 tgх.
tgх.
Получим: sinx<x<tgx (2) для 0<x<p/2.
Так как sinx>0, то разделим (2) на sinx 
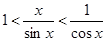
или 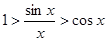 (3). Неравенство (3)выведено для 0<x<p/2, но оно верно и для -p/2<x<0:
(3). Неравенство (3)выведено для 0<x<p/2, но оно верно и для -p/2<x<0:
заменим х на –х в(3) 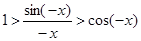 Þ
Þ 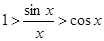 .
.
Итак, неравенство(3) выполняется для всех х из окрестности т. 0.

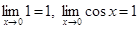 , как следует, например, из графика.
, как следует, например, из графика.
Но тогда по теореме о пределе промежуточной переменной 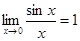 .
.
Примеры:
1) 
2) 
§11. число е.
Рассмотрим сначала переменную величину  (n=1,2,…).
(n=1,2,…).
Теорема 1. Переменная величина 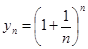 при n®¥ имеет предел, заключенный между числами 2 и 3.
при n®¥ имеет предел, заключенный между числами 2 и 3. 
Доказательство. По формуле бинома Ньютона 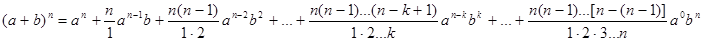 можем записать
можем записать  (1)
(1)
Преобразуем yn, упростив его: 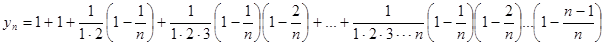 (2)
(2)
Из выражения (2) видим, что yn возрастает с возрастанием n (т.к. добавляются новые положительные слагаемые) и каждое слагаемое увеличивается, например, 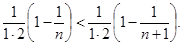 Поэтому для " n yn+1>yn. Покажем, что переменная yn ограничена сверху. Очевидно
Поэтому для " n yn+1>yn. Покажем, что переменная yn ограничена сверху. Очевидно 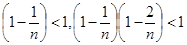 и т.д. Тогда из (2) можем записать
и т.д. Тогда из (2) можем записать  .
.
Далее 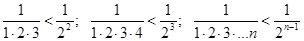 ; можем записать yn=
; можем записать yn= 
Итак, для любого n получаем, что (1+1/n)n<3, т.е. ограничена сверху. Но из (2) видно, что (1+1/n)n³2. Таким образом, для всех n имеем неравенство
2£(n+1/n)n<3. Так как величина (1+1/n)n – возрастающая и ограниченная сверху, то она имеет предел. Он не может быть больше 3-х и не может быть меньше 2-х. Этот предел обозначили числом е.
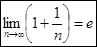 Он называется вторым замечательным пределом: 2£е£3.
Он называется вторым замечательным пределом: 2£е£3.
е называют “числом Непера” (шотландский математик). Число е, как доказано, иррациональное. Вычислено его значение с многими десятками десятичных знаков. Приведем первые десять: е=2,7182818284...
Переменную величину (1+1/n)n можно рассматривать как функцию натурального аргумента: f(n)=(1+1/n)n. При n®¥ f(n)®e. Рассмотрим функцию непрерывно меняющегося аргумента x: f(x)=(1+1/x)x.
Теорема 2. Функция (1+1/x)x при х®¥ стремится к числу е: 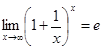 .
.
Следствие. Предел функции 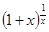 при х®0 равен числу е. Достаточно положить 1/х=у, тогда
при х®0 равен числу е. Достаточно положить 1/х=у, тогда 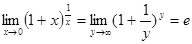 .
.
Примеры. 1) 
Короче: 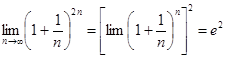 .
.
3)  .
.
§12. Понятие о гиперболических функциях.
Как увидим, число е играет важную роль в математике. В частности, важную роль играет показательная функция с основанием
е(экспонента):у=ех. Она обладает обычными свойствами показательной функции (е>1). Но с помощью этой функции определяются, например, важные в применениях гиперболические функции. Функции эти определяются следующим образом:
1) гиперболический синус: 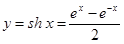

2) гиперболический косинус: 
3) гиперболический тангенс: 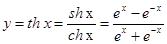
4) гиперболический котангенс: 
Функции получили название гиперболических, так как они удовлетворяют уравнению гиперболы х2-у2=1, т.е. Ch2x-Sh2x=1. (легко проверить подстановкой).
Обычные тригонометрические функции sin x и cos x называются круговыми, так как они удовлетворяют уравнению окружности х2+у2=1. Синусом, косинусом и т.д. они называются потому, что обладают многими свойствами тригонометрических функций.
Например:
1) th×cthx=1
2) sh(x+y)=shx×chx+shy×chy
3) ch(x+y)= chx×chy+shx×shy и т.п.
(проверяется подстановкой выражений через е).
 Без подробных рассуждений приведем графики функций, учитывая, что shx, chx, tgx определены на (¥,+¥), а cthх во всех х¹0. Из графиков видны основные свойства функций.
Без подробных рассуждений приведем графики функций, учитывая, что shx, chx, tgx определены на (¥,+¥), а cthх во всех х¹0. Из графиков видны основные свойства функций.

 |
§13. НАТУРАЛЬНЫЕ ЛОГАРИФМЫ
Логарифмическая функция y=logax рассматривается при любом основании a>0, a¹1. Особо выделяют логарифмическую функцию с основанием a=10: y=log10x=lgx. Такие логарифмы называются десятичными или Бригговыми (по имени английского ученого Бригга), они подробно изучались в школе. В математике и её приложениях очень часто применяются логарифмы с основанием a=e (числу Непера): y=logex=lnx. Они называются Неперовыми логарифмами или натуральными. (Непер тоже жил в 16 веке). Число y есть натуральный логарифм числа х: y=lnx, если ey=x. lne=1, т.к. e1=e. Графики натуральных и десятичных логарифмов имеют вид, обычный для логарифмической функции y=logax при a>1
Существует связь между десятичными и натуральными логарифмами одного и того же числа x>0. Установим её. Очевидно х=еlnx. Прологарифмируем по основанию 10. lgx=lnx×lge, т.к. е=2,7182818284…, то lge=0,434294. Число M=lge= 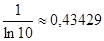

 называется модулем перехода от натуральных логарифмов к десятичным. M не зависит от x lgx=M×lnx. Переход от десятичных к натуральным:
называется модулем перехода от натуральных логарифмов к десятичным. M не зависит от x lgx=M×lnx. Переход от десятичных к натуральным: 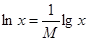 . При этом 1/M
. При этом 1/M 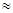 2,302584. Для вычисления десятичных и натуральных логарифмов составлены подробные таблицы этих функций, которые содержатся в справочниках по математике.
2,302584. Для вычисления десятичных и натуральных логарифмов составлены подробные таблицы этих функций, которые содержатся в справочниках по математике.
§14. СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИН.
Как и раньше мы будем говорить о б.м. функциях a(х),b(х),… от непрерывного аргумента, имея ввиду, что б.м.ф. от натурального аргумента (числовые последовательности) есть лишь частный случай и для них всё сказанное тем более верно.
Пусть имеется несколько б.м.в. a(х), b(х), g(х),…, которые являются функциями одной переменной х, стремящейся к конечному или бесконечному пределу a (a – конечное число или ¥).
В ряде вопросов очень важно знать какая величина ®0 быстрее. Например, a(х)=1/x3 стремится быстрее к 0, чем b(х)=1/x при x®¥. В других случаях это увидеть сложнее.
Определение 1. Если 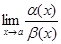 двух б.м. a(х) и b(х) равен постоянному числу c¹0, то эти б.м.в. называются б.м. одного порядка (малости). Символически a(х)=О(b(х)).
двух б.м. a(х) и b(х) равен постоянному числу c¹0, то эти б.м.в. называются б.м. одного порядка (малости). Символически a(х)=О(b(х)).
Пример: 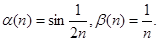
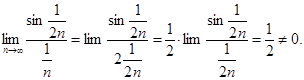
a(n) и b(n) одного порядка малости sin1/2n=O(1/n).
Определение 2. Если 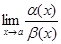 двух б.м.в. равен нулю, то a(х) называется б.м. высшего порядка (малости), чем b(х), а b(х) нижнего порядка малости, чем a(х). Записывают
двух б.м.в. равен нулю, то a(х) называется б.м. высшего порядка (малости), чем b(х), а b(х) нижнего порядка малости, чем a(х). Записывают 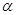 (x)= o(b(x)).
(x)= o(b(x)).
Например: 1/x3=o(1/x), 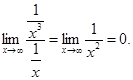
Определение 3. Если существует при х®а бесконечный предел отношения a(х)/b(x), то b(х)=о(a(х)). Если не существует при x®a ни конечного, ни бесконечного предела отношения a(х)/b(x), то они называются несравнимыми.
Пример: a(х)=х×sin1/x,  (x)=x, при х®0 они б.м.в.,
(x)=x, при х®0 они б.м.в.,
т.к. a(х)®0 (б.м.в. на ограниченную)
b(х)®0.
Но 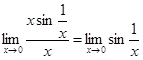 не существует, a(х) и b(х) несравнимые б.м.в.
не существует, a(х) и b(х) несравнимые б.м.в.
Бывает важно сравнить точно порядки малости сравниваемых б.м.в., выражая их числом.
Определение 4. a(х) называется б.м. к-ого порядка по сравнению с б.м. b(х), если  (с – конечное число).
(с – конечное число).
Пример. a(x)=1/x3. b(x)=1/x. 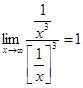 => 1/x3 б.м. к=3 малости по сравнению с 1/x.
=> 1/x3 б.м. к=3 малости по сравнению с 1/x.
§15. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ВЕЛИЧИНЫ.
Определение 5. Б.м.в. a(х) и b(х) называются эквивалентными б.м., если предел их отношения при х®а равен 1, т.е. 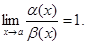
Обозначим a(х)  b(х). Например, sinx ¥ x при х®0, т.к.
b(х). Например, sinx ¥ x при х®0, т.к. 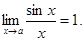
Теорема. Для того, чтобы б.м.в. a(х) и b(х) были эквивалентными, необходимо и достаточно, чтобы их разность g(х)=a(х)-b(х) была б.м.в. высшего порядка, чем a(х) и чем b(х).
Доказательство: I Н-ть. Пусть a(х)¥ b(х), т.е. 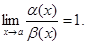 Тогда
Тогда 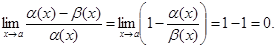
 g(х)=о(a(х)).Аналогично, показывается, что g(х)=о(b(х)).
g(х)=о(a(х)).Аналогично, показывается, что g(х)=о(b(х)).
II. Достаточность. Пусть a(х)-b(х)=о(b(х)), т.е. 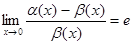
Тогда 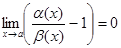 =>
=> 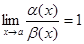 . -> a(x)¥ b(x).
. -> a(x)¥ b(x).
Приведем некоторые другие пары эквивалентных б.м.в. (все при х®0), кроме sinx ¥ x.
1) 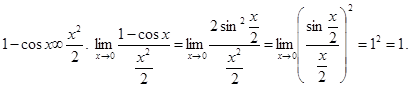
2) 
3) 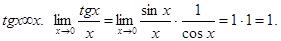
4)  Положим y=ex-1. Тогда при х®0 и y®0. ех=y+1. х=ln(y+1). Тогда
Положим y=ex-1. Тогда при х®0 и y®0. ех=y+1. х=ln(y+1). Тогда 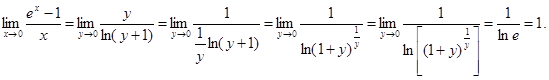 (Использован факт, что знак предела и непрерывной функции можно менять местами – будет доказано позднее).
(Использован факт, что знак предела и непрерывной функции можно менять местами – будет доказано позднее).
5) 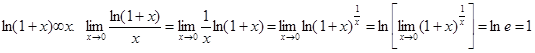 /ч.т.д.
/ч.т.д.
Из определения эквивалентных б.м.в. видно, что при х, достаточно близких к а, значения эквивалентных б.м.в. становятся сколь угодно близкими и их можно на практике заменить одна другой. Отсюда приближённые формулы. При малых х (близких к нулю) можем считать sinx»x; 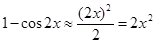 ;
; 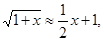 tgx»x, ex»x+1, ln(1+x)»x и т.п. Ими с успехом пользуются в приближённых вычислениях.
tgx»x, ex»x+1, ln(1+x)»x и т.п. Ими с успехом пользуются в приближённых вычислениях.
Например.
1) 
(все цифры верные)
2) 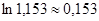 (в действительности 0,142)
(в действительности 0,142)
Применяются эквивалентные б.м.в. и при вычислении пределов. Основой является:
Теорема. Если имеем две пары б.м.в. при х®a a(х),b(х), a1(х),b1(х), причем a(х)
