Двухполостный гиперболоид.
Если вращать гиперболу 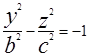 вокруг оси OZ, то в результате получим двухполостный гиперболоид вращения.
вокруг оси OZ, то в результате получим двухполостный гиперболоид вращения. 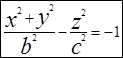 (1) Если растянуть его по оси ОХ в к раз, то получим общий вид двухполостного гиперболоида. Его каноническое уравнение
(1) Если растянуть его по оси ОХ в к раз, то получим общий вид двухполостного гиперболоида. Его каноническое уравнение 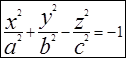 (2), где а=kb. Если пересекать двухполостный гиперболоид плоскостями z=h (h>c), в сечении получим эллипсы
(2), где а=kb. Если пересекать двухполостный гиперболоид плоскостями z=h (h>c), в сечении получим эллипсы 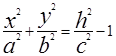 или
или 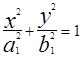 , где
, где 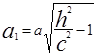 ,
, 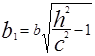 . При бесконечном возрастании h
. При бесконечном возрастании h
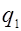 и
и 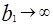 , эллипсы увеличиваются ; при h=c
, эллипсы увеличиваются ; при h=c 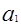 и
и 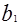 =0, эллипсы стягиваются в точку; при
=0, эллипсы стягиваются в точку; при 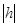 <c.
<c. 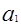 и
и 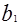 имют мнимые значения, пересечений нет.
имют мнимые значения, пересечений нет.
Если пересекать плоскостями x=h или y=h получим в сечении гиперболы 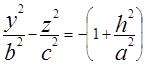 или
или 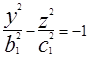
|
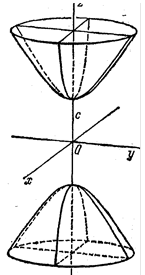
Из сказанного ясно, что двухполостный гиперболоид состоит из двух бесконечных кусков - полостей, отстоящих одна от другой на 2с. Двухполостный гиперболоид имеет три плоскости симметрии - координатные плоскости.
Конус.
 |
Если вращать прямую
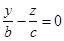 вокруг оси ОZ, в результате получим поверхность называемую конической или конусом, он называется круговым. Уравнение конуса будет
вокруг оси ОZ, в результате получим поверхность называемую конической или конусом, он называется круговым. Уравнение конуса будет 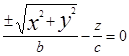 или
или 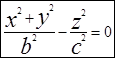 (1). Если растянуть конус по оси ОХ в к раз, получим общий конус второго порядка. Его каноническое уравнение
(1). Если растянуть конус по оси ОХ в к раз, получим общий конус второго порядка. Его каноническое уравнение 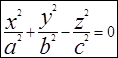 (2), где а=kb. Очевидно, в сечении конуса плоскостями z=h получаются эллипсы, а плоскостями x=h или y=h - гиперболы.
(2), где а=kb. Очевидно, в сечении конуса плоскостями z=h получаются эллипсы, а плоскостями x=h или y=h - гиперболы.
Нетрудно доказать, что образующими общего конуса непременно являются прямые линии.
Докажем, что если некоторая точка 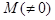 лежит на конусе (2), то и вся прямая , проходящая через М и О лежит на конусе.
лежит на конусе (2), то и вся прямая , проходящая через М и О лежит на конусе.
Пусть М имеет координаты (m,n,l). Тогда вектор 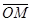 является направляющим вектором прямой
является направляющим вектором прямой 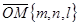 . Точка О(0,0,0) лежит на прямой. Поэтому параметрическое уравнение прямой x=mt, y=nt, z=lt. (3) Т.к. точка М лежит на конусе, то её координаты удовлетворяют уравнению (2):
. Точка О(0,0,0) лежит на прямой. Поэтому параметрическое уравнение прямой x=mt, y=nt, z=lt. (3) Т.к. точка М лежит на конусе, то её координаты удовлетворяют уравнению (2): 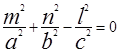 .
.
Возьмём точку N(x,y,z) на ОМ. (xyz) выразятся уравнениями (3). Но тогда 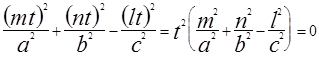 . Значит и
. Значит и 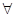 т. N прямой OM
т. N прямой OM 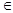 конусу.
конусу.
Дата добавления: 2015-10-05; просмотров: 1410;
