Уравнение поверхности вращения.

Некоторые поверхности 2го порядка являются поверхностями вращения. Пусть в плоскости YOZ лежит некоторая кривая L F(y,z)=0(1). Выясним, каково будет уравнение поверхности S, образованной вращением кривой (1) вокруг оси oz.

Возьмем на поверхности S произвольную точку M(x,y,z). Ее можно считать полученной из (.) N принадлежащей L , тогда аппликаты точек M и N равны (=z). Ордината точки N 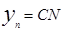является тут радиусом вращения, потому 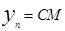. Но С(0,0,z) и потому 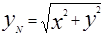. Но точка N лежит на кривой и поэтому её координаты ей удовлетворяют. Значит 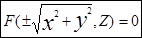(2). Уравнению (2) удовлетворяют координаты 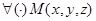поверхности вращения S. Значит (2) и есть уравнение поверхности вращения. Знаки «+» или «-» берутся в зависимости от того в какой части плоскости YOZ размещается кривая (1), где у>0 или .

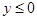Итак, правило: Чтобы найти уравнение поверхности, образованной вращением кривой L вокруг оси OZ, нужно в уравнении кривой заменить переменную у

на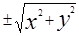

Аналогично составляются уравнения поверхностей вращения вокруг оси OX и OY.