КРИВЫЕ ВТОРОГО ПОРЯДКА
1. Порядок кривой.
Как мы знаем, уравнение любой кривой на плоскости ОХУ имеет вид F(x,y)=0. Если F(x,y) есть многочлен с двумя переменными, то уравнение имеет вид
A1xm1yn1+A2xm2yn2+…+Akxmkynk=0. (1)
Линия, определяемая таким уравнением, называется алгебраической линией. Степень (или порядок) многочлена в уравнении (1) называют порядком линии, которую оно определяет. Напомним, что порядком многочлена называют max {mi+ni}, т.е. наибольшую из степеней одночленов, составляющих многочлен.
Мы уже знаем, что существует только одна линия первого порядка на плоскости—прямая линия. Ее уравнение
Ax+By+C=0.
Самый общий вид уравнения линий второго порядка есть
Ax2+2Bxy+Cy2+2Dx+2Ey+F=0. (2)
Линий второго порядка уже значительно больше. Самыми важными из них являются: окружность, эллипс, гипербола, парабола.
Изучим эти кривые более подробно.
2. Окружность.
Окружность—геометрическое место точек (ГМТ) плоскости, удаленных на одно и то же расстояние r от одной точки C.
Мы уже знаем, что уравнение любой окружности радиуса r с центром С(x0,y0) имеет вид(x-x0)2+(y-y0)2=r2.
Отсюда видно, что окружность есть линия второго порядка. Раскрыв скобки, мы получим
x2+y2+2x0x+2y0y+(x02+y02-r2)=0 (3)
Это уравнение второго порядка. Сравнение (3) и (2) показывает особенности уравнения окружности:
1) коэффициенты при x2 и y2 равны (А=С);
2) член с произведением xy отсутствует (В=0).
Оказывается, что и, вообще, любое уравнение вида (2), где А=С и В=0, т.е.
Ax2+Ay2+2Dx+2Ey+F=0 (4) является уравнением окружности (или, вообще, ничего не определяет).
Уравнение (4) можно привести к стандартному уравнению окружности:
 A(x2+2
A(x2+2 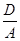 x+
x+ 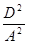 )+A(y2+2
)+A(y2+2 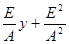 )=
)= 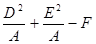
(выделим полные квадраты по переменным х и у),
или A(x+ 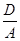 )2+A(y+
)2+A(y+ 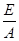 )2=P.
)2=P.
Разделим почленно это равенство на А и обозначим Р/А=R2:
(x+ 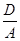 )2+(y+
)2+(y+ 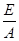 )2=R2. (5)
)2=R2. (5)
Это уравнение окружности с радиусом R и центром C( 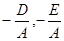 ).
).
Если 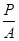 <0, то уравнение (4), вообще, не задает никакую линию.
<0, то уравнение (4), вообще, не задает никакую линию.
3.Определение и вывод канонического уравнения эллипса.
Эллипсом называют ГМТ плоскости, для которых сумма расстояний от двух данных точек F1 и F2, называемых фокусами, есть величина постоянная (большая, чем расстояние между фокусами).
Будем обозначать расстояние между фокусами F1F2=2с, а сумму расстояний 2а, (а>с). Чтобы вывести уравнение эллипса, исходя из его определения, выберем систему координат наиболее удобным образом (чтобы уравнение его было наиболее простым).
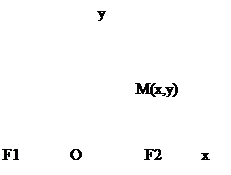
Проведем ось ОХ через фокусы F1 и F2, а начало координат поместим в середине отрезка F1F2. Возьмем точку М (х,у)О эллипсу. Отрезки r1=F1M и r2=F2M называем фокальными радиусами точки М. Тогда F1M+F2M=2a. Координаты фокусов в этой системе, очевидно, будут F1 (-c;0), F2 (c;0). Тогда можем записать: 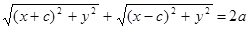 --(1)—это и есть уравнение эллипса в выбранной системе координат. Упростим это уравнение. Уединим один радикал и возведем в квадрат равенство:
--(1)—это и есть уравнение эллипса в выбранной системе координат. Упростим это уравнение. Уединим один радикал и возведем в квадрат равенство: 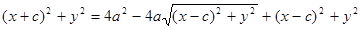 или
или 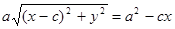 . Снова возведем в квадрат:
. Снова возведем в квадрат: 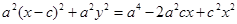 или
или 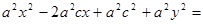
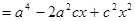 или
или 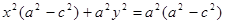 . Разделим это уравнение на
. Разделим это уравнение на
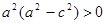 . Получим
. Получим 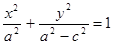 . Обозначим
. Обозначим 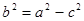 , тогда
, тогда

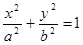 (2) –это и есть каноническое
(2) –это и есть каноническое
Дата добавления: 2015-10-05; просмотров: 1594;
