Прямая линия и плоскость
КАФЕДРА МАТЕМАТИЧЕСКОГО АНАЛИЗА
В.А. БАЙКОВ
к.ф.-м.н., доцент кафедры математического анализа ТулГУ
МАТЕМАТИКА
Конспект лекций
для студентов направлений горно-строительного профиля
Часть первая
Тула, 2000 г.
СОДЕРЖАНИЕ
| Аналитическая геометрия и элементы линейной алгебры | ||
| Ведение в математический анализ | ||
| Дифференциальное исчисление функций одной переменной | ||
| Функции нескольких переменных | ||
| Интегральное исчисление функций одной переменной | ||
| Ряды |
Аналитическая геометрия и элементы линейной алгебры.
План.
Векторная алгебра и метод координат.
§1. Скалярные и векторные величины. 5
§2. Коллинеарные, равные, компланарные векторы. 5
§3. Линейные операции над векторами. 6
§4. Свойства линейных операций. 8
§5. Разложение вектора по базису. Координаты вектора. 8
§6. Линейная зависимость векторов. 10
§7. Декартова система координат. 10
§8. Линейные пространства. 11
§9. Скалярные произведения векторов. 13
§10. Евклидово пространство. 15
§11. Векторное произведение двух векторов 17
§12. Смешанное произведение трех векторов. 19
Прямая линия и плоскость.
§1. Понятие уравнения линии и поверхности. 21
§2. Уравнения плоскости, уравнения прямой на плоскости и в
пространстве. 23
§3. Условия параллельности и перпендикулярности прямых и
плоскостей. 27
§4. Основные задачи о прямых и плоскостях. 28
Кривые второго порядка.
§1. Порядок кривой. 31
§2. Окружность. 32
§3. Определение и вывод канонического уравнения эллипса. 32
§4. Исследование формы эллипса по его каноническому уравнению. 34
§5.Определение и вывод канонического уравнения гиперболы. 36
§6. Исследование формы гиперболы по ее каноническому уравнению. 37
§7. Определение и вывод канонического уравнения параболы. 39
§8. Исследование формы параболы по ее каноническому уравнению. 40
Матрицы и их применение.
§1. Основные определения. Действия над матрицами. 42
§2. Понятие ранга матрицы. 45
§3. Понятие об обратной матрице. 47
§4. Решение систем линейных уравнений с помощью обратной
матрицы. 48
§5. Решение систем линейных уравнений методом исключения
неизвестных (метод Гаусса). 49
§6. Линейные преобразования на плоскости ив пространстве. 52
§7. Собственные векторы и собственные числа матрицы
(линейного преобразования). 53
§8. Собственные числа и собственные векторы в случае
симметричной матрицы. 55
§9. Приведение квадратичной формы к каноническому виду. 56
§10. Приведение общего уравнения второго порядка к
каноническому виду. 57
Поверхности второго порядка.
§1. Порядок поверхности. 60
§2. Цилиндрические поверхности с образующими, параллельными
одной из координатных осей. 60
§3. Уравнение поверхности вращения. 62
§4. Сжатие и растяжение поверхностей. 63
§5. Эллипсоид. 63
§6. Однополостный гиперболоид. 64
§7. Двухполостный гиперболоид. 65
§8. Конус. 66
§9. Эллиптический параболоид. 67
§10. Гиперболический параболоид. 68
I. Аналитическая геометрия и элементы линейной алгебры.
1. Векторная алгебра и метод координат.
§1. Скалярные и векторные величины.
Величины бывают двух видов: скалярные (температура, масса, объём, количество электричества и т.д.) и векторные (сила, ускоре 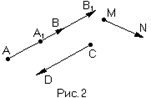 ние, скорость, напряженность электромагнитного поля и т.д.). Каждая скалярная величина вполне может быть охарактеризована одним числом (количеством), выражающим отношение её к соответствующей единице измерения (20 кг, 5 м3 и т.д.). Векторную же величину одним числом полностью охарактеризовать нельзя. Векторная величина кроме количественной характеристики должна иметь и направление. Сказать, что скорость движения точки равна 5 м/сек ещё мало, нужно указать направление скорости.
ние, скорость, напряженность электромагнитного поля и т.д.). Каждая скалярная величина вполне может быть охарактеризована одним числом (количеством), выражающим отношение её к соответствующей единице измерения (20 кг, 5 м3 и т.д.). Векторную же величину одним числом полностью охарактеризовать нельзя. Векторная величина кроме количественной характеристики должна иметь и направление. Сказать, что скорость движения точки равна 5 м/сек ещё мало, нужно указать направление скорости.
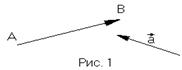 В математике с целью достижения наибольшей общности отвлекаются от конкретных векторных величин и изучают геометрические векторы или просто векторы, под которыми понимают направленные отрезки. Если отрезок ограничен точками А и В и сказано, какую точку считать началом и какую концом его, то он называется направленным, а направление от начала к концу его называется направление отрезка или, все равно, вектора. Изображают вектор стрелочкой, ставя заглавные латинские буквы начала и конца, а иногда только одну прописную посередине (рис. 1).
В математике с целью достижения наибольшей общности отвлекаются от конкретных векторных величин и изучают геометрические векторы или просто векторы, под которыми понимают направленные отрезки. Если отрезок ограничен точками А и В и сказано, какую точку считать началом и какую концом его, то он называется направленным, а направление от начала к концу его называется направление отрезка или, все равно, вектора. Изображают вектор стрелочкой, ставя заглавные латинские буквы начала и конца, а иногда только одну прописную посередине (рис. 1).
На письме обозначают 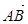 или
или 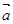 (в книгах иногда стрелки не ставят, т.к. используют «жирный» (выделенный) шрифт для обозначения векторов.)
(в книгах иногда стрелки не ставят, т.к. используют «жирный» (выделенный) шрифт для обозначения векторов.)
Длину (модуль) вектора АВ (или а) обозначают 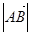 (или
(или  ), понимая под ним обычную длину отрезка АВ.
), понимая под ним обычную длину отрезка АВ.
Над векторами производят некоторые операции, напоминающие операции над числами и буквами в обычной алгебре. Раздел аналитической геометрии, где изучаются эти операции и их законы часто называют векторной алгеброй.
§2. Коллинеарные, равные, компланарные векторы.
Определение. Векторы, лежащие на одной прямой или на параллельных прямых называются коллинеарными.
Обозначают: АВ || А1В1, АВ || CD ,
АВне || MN (см. Рис. 2)
Определение. Векторы называются равными, если 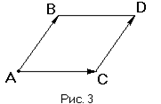 они:
они:
1) Коллинеарны;
2) Имеют равные модули;
3) Одинаково направлены.
Пишут: AB = CD , но AB ¹ AC (рис. 3)
Часто равные вектора не различают между собой, считая, что это один и тот же вектор только с разной точкой приложения (разным началом). В этом смысле геометрические вектора называют свободными. Если же начало определённое, то вектор называется связанным.
Если за начало вектора можно взять любую точку некоторой кривой, то вектор называется скользящим. (Рис. 4)
Определение: Три вектора называются компланарными, если они 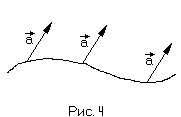 лежат в некоторой одной плоскости или параллельны какой-то одной плоскости.
лежат в некоторой одной плоскости или параллельны какой-то одной плоскости.
Заметим, что параллельным переносом (векторы же свободные!) компланарные векторы всегда можно поместить в одну плоскость. (Ри 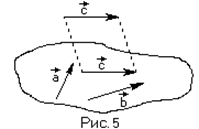 с. 5)
с. 5)
Примером некомпланарной тройки векторов могут служить направленные рёбра куба, исходящие из одной вершины.
§3. Линейные операции над векторами.
Над векторами производят различные действия (операции). В этом параграфе рассмотрим операции: умножение вектора на скаляр (число) и сложение векторов, которые называют линейными операциями.
1) Умножение вектора на скаляр.
Пусть имеется вектор а, обозначающий, например, скорость движения точки. Тогда 2а означает вдвое большую скорость движения в том же направлении, а (-1/2)а означает вдвое меньшую скорость движения в противоположенном направлении.
Определение: Произведением вектора а на скаляр m называется вектор b, который:
1) имеет модуль |b|=|m|×|a|;
2) коллинеарен вектору а;
3) направлен так же как вектор а при m>0 и противоположено вектору а при m<0.
Обозначается произведение b=ma, причем ma=am, как следует из определения.
В частности, при m=-1 имеем (-1)×а. Вектор -аназ 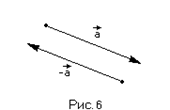 ывается противоположенным вектору а (рис. 6)
ывается противоположенным вектору а (рис. 6)
Если а=0 или m=0, то m×а=0 – нулевой вектор. Ему не приписывается никакого определенного направления (начало и конец совпали!).
Деление вектора на число m¹0 равносильно умножению его на число (1/m), т.е.
Геометрический смысл операции умножения вектора а на число m состоит в "растяжении" вектора а в m раз, (если |m|>1, то это действительно растяжение, а при |m|<1, – это сжатие) с возможным изменением направления.
Если |e|=1, то вектор e называется единичным вектором (ортом)
Легко видно, что вектор а=а°×|a|, если а° единичный вектор (орт) вектора а.
Отметим важный факт:
Если два вектора a и b коллинеарны, то один из них (любой) линейно выражается через другой: 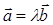 (или
(или 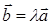 ). Очевидно
). Очевидно 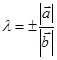
"+" если а и bнаправлены одинаково;
"–" если противоположено.
Такое представление однозначно.
2) Сложение векторов.
Правило сложения векторов есть обобщение обычног 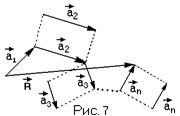 о правила сложения сил, скоростей и т.п. в механике. Пусть даны векторы а1,а2,а3,…,аn произвольно расположенные в пространстве. Перемещая их параллельно самим себе (векторы свободные!) векторы всегда можно расположить в виде ломаной, когда конец предыдущего вектора является началом следующего (Рис. 7)
о правила сложения сил, скоростей и т.п. в механике. Пусть даны векторы а1,а2,а3,…,аn произвольно расположенные в пространстве. Перемещая их параллельно самим себе (векторы свободные!) векторы всегда можно расположить в виде ломаной, когда конец предыдущего вектора является началом следующего (Рис. 7)
Определение:Суммой векторов а1,а2,а3,…,аnназывается вектор R, замыкающий ломаную линию, построенную из них указанным образом, причем начало его в начале вектора а1, конец в конце вектора аn
Обозначают: R= а1+а2+а3+…+аn
Из этого общего правила легко следует удоб 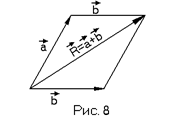 ное правило параллелограмма для нахождения суммы двух векторов: сумма двух векторов a и b, приведённых к одному началу О, есть вектор–диагональ параллелограмма, построенного на векторах a и b как на сторонах (Рис. 8)
ное правило параллелограмма для нахождения суммы двух векторов: сумма двух векторов a и b, приведённых к одному началу О, есть вектор–диагональ параллелограмма, построенного на векторах a и b как на сторонах (Рис. 8)
Из рисунка 8 видно, что вектор–диагональ R=a+b является замыканием ломаной из векторов a и b, что согласуется с общим правилом сложения.
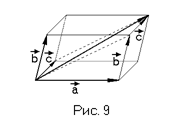 Из общего же правила следует и правило параллелепипеда нахождения суммы трех векторов, приведенных в одно начало О (и не компланарных): это есть вектор–диагональ параллелепипеда, построенного на данных векторах, как на сторонах (Рис. 9).
Из общего же правила следует и правило параллелепипеда нахождения суммы трех векторов, приведенных в одно начало О (и не компланарных): это есть вектор–диагональ параллелепипеда, построенного на данных векторах, как на сторонах (Рис. 9).
3) Вычитание векторов.
Операция вычитания векторов a и b (обозначается a-b) понимается как сложение вектора a с вектором -b, противоположенным вектору b.
На практике по векторам a и b, приведённым в одно начало О, сразу строят вектор BA=a-b, как идущий из конца вычитаемого вектора b в конец ум 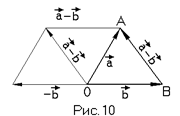 еньшаемого вектора а. (Рис. 10)
еньшаемого вектора а. (Рис. 10)
§4. Свойства линейных операций.
Отметим восемь основных свойств линейных операций над векторами:
1) a+b=b+a (коммутативность сложения или переместительность)
2) a+(b+c)=(a+b)+c(ассоциативность сложения или сочетательность)
3) a+0=a.
4) Для любого вектора aсуществует ему противоположенный вектор –a, так что a+(–a)=0
5) 1×a=a
6) m(n×a)=(m×n)×a(ассоциативность умножения на скаляр)
7) m(a+b)=m×a+m×b(распределительные свойства относи-
8) (m+n)×a=m×a+n×aтельноумножения на скаляр)
Справедливость свойств 3–5 для геометрических векторов очевидны. Справедливость свойств 1 и 2 следует из самого определения суммы двух векторов. (диагональ параллелограмма одна и та же для a+b и для b+a) (Рис. 11)
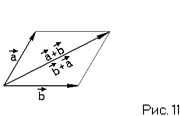 |  |
Свойство 6 и 8 следует из истолкования умножения вектора на скаляр m как "растяжения" его в |m| раз с возможным изменением направления на противоположенное. Свойство 7 следует из подобия треугольников. (Рис. 12)
 |  | 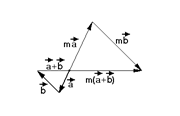 |
§5. Разложение вектора по базису. Координаты вектора.
Рассмотрим систему n векторов а1,а2,а3,…,аn. Каждый вектор вида α1а1+α2а2+α3а3+…+αnаn , где α1, α2, α3,…, αn некоторые действительные числа, называется линейной комбинацией данных векторов, числа α1, α2, α3,…, αnназываются коэффициентами этой линейной комбинации. Линейная комбинация называется нетривиальной, если хотя бы один коэффициент αк ¹ 0 (в противном случае она называется тривиальной).
Если некоторый вектор d представить в виде определённой комбинации данных векторов. d=α1а1+α2а2+α3а3+…+αnаn то говорят, что вектор d разложен по системе векторов 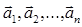 .
.
Теорема 1. Если e1 и e2 два неколлинеарных вектора, то всякий компланарный с ними третий вектор d раскладывается по ним и это разложение единственно.
Теорема 2. Если e1,e2,e3 три некомпланарные вектора, то всякий четвертый в 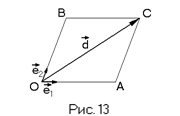 ектор d раскладывается по ним и это разложение единственно.
ектор d раскладывается по ним и это разложение единственно.
Доказательство теорем совершенно аналогично. Для краткости докажем теорему 1. Приведем вектора e1, e2 и dв одно начало О и построим параллелограмм, стороны которого лежат на векторах e1, e2, а вектор dявляется его диагональю. (Рис. 13)
Очевидно d=OC=OA+OB. Но OA || e1 => OA=me1, OB|| e2 =>OB=ne1. Тогда d=me1+ne2 – разложение получено и оно единственно, т.к. n и m определяются однозначно.
Определение: Любые два неколлинеарных упорядоченных (взятых в определенном порядке) вектора на плоскости называются базисом на этой плоскости.
Любые три некомпланарные упорядоченные вектора в пространстве называются базисом в пространстве.
Из сказанного выше следует (например, в пространстве), что задание базиса однозначно сопоставляет каждому вектору d тройку чисел {α, β, γ} – его коэффициенты разложения по этому базису, и наоборот: каждой упорядоченной тройке чисел {α, β, γ} при помощи базиса сопоставляется вполне определённый вектор d=αe1+βe2+γe3 .
По этому введём:
Определение: Если вектора e1,e2,e3 – базис и вектор а=αe1+βe2+γe3 , то числа α, β, γ называются координатами (компонентами) вектора а в этом базисе.
Символически будем писать вектор а={α, β, γ}(e1,e2,e3) или просто а={α, β, γ}.
Теорема 3. Над координатами векторов производятся те же линейные операции, что и над самими векторами.
Доказательство:
Пусть вектор а={α, β, γ}(e1,e2,e3). Это означает а=αe1+βe2+γe3.
Но тогда mа=m(αe1+βe2+γe3) = (mα)e1+(mβ)e2+(mγ)e3
Откуда следует, что вектор mа={mα, mβ, mγ}(e1,e2,e3)
Пусть вектор b={α1, β1, γ1} тогда
a±b=(αe1+βe2+γe3)±(α1e1+β1e2+γ1e3) =
= (α±α1)e1+(β±β1)e2+(γ±γ1)e3
отсюда следует, что a±b= {α±α1, β±β1, γ±γ1}.
§6. Линейная зависимость векторов.
Линейная комбинация нескольких векторов называется тривиальной, если все её коэффициенты равны нулю. Очевидно она равна нулю. Линейная комбинация называется нетривиальной, если хоть один коэффициент не равен нулю.
Определение: Векторы a1, a2, … ,an называются линейно зависимыми, если существует нетривиальная линейная комбинация этих векторов, равная 0.
Если же только тривиальная линейная комбинация векторов равна 0 для этих векторов, то они называются линейно независимыми. Для линейно независимых векторов из
α1а1+α2а2+ …+αnаn = 0 => α1=α2=…=αn=0.
Оказываются справедливыми теоремы:
Теорема 1: Любые два коллинеарные вектора линейно зависимы. Любые два неколлинеарные вектора линейно независимы.
Теорема 2: Три компланарных вектора линейно зависимы, а любые три некомпланарные вектора линейно независимы.
Теорема 3: Каждые четыре вектора в пространстве линейно зависимы. Либо все они компланарны, тогда они линейно зависимы. Если они некомпланарны, тогда один из них линейно выражается через три других. (=> линейно зависимы.)
Замечание: Базисы на плоскости и в пространстве состоят из линейно независимых систем векторов.
§7. Декартова система координат.
Фиксируем в пространстве точку О и рассмотрим произвольную точку M. OM – радиус-вектор точки M.
Если в пространстве имеем базис e1,e2,e3, то точке М можно сопоставить тройку чисел – координат (компонент) радиус-вектора ОМ.
Определение: Декартовой системой координат в пространстве называется совокупность базиса и точки.
Точка О называется началом координат, прямые, проходящие в направлении базисных векторов называются осями координат.
 Плоскости, проходящие через оси, называются координатными плоскостями.
Плоскости, проходящие через оси, называются координатными плоскостями.
Определение: Координаты радиус-вектора точки М по отношению к началу координат называются координатами точки М в этой системе координат.
ОМ=xe1 +ye2 + ze3. Тогда М(x,y,z).
Аналогично на плоскости.
При заданной системе координат:
1) Каждой точке М соответствует единственная тройка чисел (её координат).
2) Каждой тройке чисел соответствует определённая точка М.
Задача 1 В системе координат О,e1,e2,e3 заданы координаты начала и конца вектора АВ : А(x1,y1,z1), В(x2,y2,z2).
Найти координаты вектора АВ.
Решение: 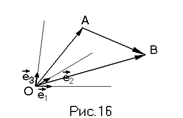
АВ=ОВ-ОА, но ОВ={x2,y2,z2}, ОА={x1,y1,z1}.
Тогда АВ={ x2- x1, y2- y1, z2- z1 }.
Определение: Чтобы найти координаты вектора нужно из координат его конца вычесть соответствующие координаты начала.
Задача 2 А(x1,y1,  z1), В(x2,y2,z2). Разделить отрезок АВ в отношении l. Найти координаты т. М(x,y,z), делящей AB в отношении l.
z1), В(x2,y2,z2). Разделить отрезок АВ в отношении l. Найти координаты т. М(x,y,z), делящей AB в отношении l.
Т. е. AM / MB =l. l>0 => AM =l×MB.
AM = {x-x1, y-y1, z-z1}; MB = {x2-x, y2-y, z2-z}
Тогда (x-x1)=l(x2-x); (y-y1)=l(y2-y); (z-z1)=l(z2-z);
=> 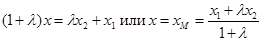
Аналогично: 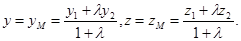
Замечание: Если М=С – середина отрезка, то l=1 =>
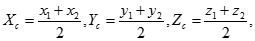
§8. Линейные пространства.
Мы рассмотрели множество геометрических векторов (направленных отрезков) и ввели в нем линейные операции (сложение и умножение на число), удовлетворяющие отмеченным свойствам. Оказывается, можно рассматривать и множества других объектов (чисел, матриц, функций и т.д.), в которых можно ввести аналогичные операции с аналогичными свойствами. Отвлечемся от конкретных свойств элементов, и будем рассматривать, так называемые, линейные пространства (иногда по аналогии с множеством обычных векторов их называют также векторными).
Определение: множество Z называется линейным пространством, а его элементы векторами, если:
а) задан закон (операция сложения), по которому любым двум элементам x,y Î Z сопоставляется элемент из множества Z, называемый их суммой и обозначаемый x+y;
б) задан закон (операция умножения на число), по которому любому x Î Z и числу α сопоставляется элемент из Z, называемый произведением x на α и обозначаемый αx.
в) для любых элементов x,y,z Î Z и любых чисел α, β выполнены следующие требования (аксиомы линейного пространства):
1) x+y = y+x
2) (x+y)+z = x+(y+z)
3) Существует элемент О такой, что для любого x Î Z выполняется равенство x+O = x
4) Для каждого x существует элемент “-x” такой, что x+(-x) = 0
5) α (x + y) = αx + αy
6) (α + β) x = αx + βx
7) α (β x) = (α β) x
8) 1×x = x
Примечание: если в б) число α лишь вещественное, то линейное пространство называется вещественным. Если α – комплексное, то Z – называется комплексным линейным пространством.
Здесь “-x” часто называется элементом противоположенным x (для “-x” противоположенным будет -(-x) = x )
O – называется нулевым элементом или нулем.
1) Обычное векторное пространство геометрических векторов будет линейным пространством.
2) Множество комплексных чисел будет линейным вещественным пространством ( если α – действительное).
3) Есть линейное пространство из одного элемента «0» с операциями: 0+0 = 0; α×0 = 0
Как и в пространстве обычных векторов в линейном пространстве можно определить понятия разности векторов, линейных комбинаций, линейной независимости и зависимости системы векторов. Сформулируем важные факты:
Если некоторые из векторов, входящих в систему, сами образуют зависимую подсистему, то и вся система линейно зависима.
Если вся система линейно независима, то и всякая её подсистема также линейно независима.
Определение:Базисом в пространстве Z называется любая система векторов, если:
А) она линейно независима;
Б) каждый вектор из Z есть линейная комбинация векторов этой системы.
Отсюда следует, что базис состоит из максимального числа линейно независимых векторов в этом пространстве. Коэффициенты линейной комбинации для любого вектора называются его компонентами (или координатами). Они для каждого вектора в данном базисе определяются однозначно.
Примем без доказательства теорему:
Теорема: Если в линейном пространстве существует базис из n векторов, то любой другой базис в этом пространстве состоит тоже из n векторов.
Определение: Линейное пространство, в котором существует базис из n векторов, называется n-мерным, а число n-размерностью пространства.
В 0-вом пространстве нет базиса и оно считается имеющим размерность 0.
Множество векторов на плоскости является 2-х мерным.
Обозначается L2 (R2)
Множество векторов в пространстве является 3-х мерным.
Обозначается L3 (R3)
Есть линейные пространства, в которых для любого натурального m найдется система m векторов, линейно независимая. Такое пространство называется бесконечномерным. Базиса в нем нет.
§9. Скалярное произведение векторов.
Вернемся в обычное векторное пространство геометрических векторов. 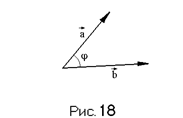
Имеются два вектора a и b. Угол между ними – это наименьший из двух углов (для векторов, приведённых в одно начало) обозначают j = (a ^ b) 0£j£p (см. рис 18)
Если j=p/2, то такие вектора называются ортогональными.
Определение: Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначается скалярное произведение (a , b)
Итак (a , b) = |a ||b |cos j, где j = (a ^ b)
Очевидны свойства скалярного произведения:
1) (a , b) = (b , a) (коммутативность)
2) (a , a) = |a|2 для любого a.
3) Скалярное произведение двух векторов равно 0 тогда и только тогда, когда сомножители ортогональны или хоть один из них равен 0.
4) Для любых векторов a, b и c и любых чисел α и β выполнимо равенство:
(αa + βb, c) = α(a , c) + β(b , c).
В частности (αa , c) = α(a , c); (a + b, c) = (a , c) + (b, c).
(без доказательства)
Пользуясь свойством 4, найдем выражение скалярного произведения двух векторов.
a = {α1, α2, α3 } и b= { β1, β2, β3 } в базисе e1, e2, e3 .
(a , b) = ({α1e1 + α2e2 + α3e3 } , { β1e1 + β2e2 + β3e3 } ) =
= α1 β1 (e1, e1) + α2 β2 (e2, e2) + α3 β3 (e3, e3) +
+ ( α1 β2 + α2 β1 )(e1, e2) + ( α1 β3 + α3 β1 )(e1, e3) + (1)
+ ( α2 β3 + α3 β2 )(e2, e3).
Определение: Базис называется ортонормированным, если его векторы попарно перпендикулярны, и их длины равны 1.
Тогда (e1, e1) = (e2, e2) = (e3, e3) = 1.
и (e1, e2) = (e1, e3) = (e2, e3) = 0. (2)
Теорема: Если базис ортонормированный, то скалярное произведение векторов выражается через их компоненты по формуле:
(a , b) = α1 β1 + α2 β2 + α3 β3 . (3)
Доказательство: подставим (2) в (1)
Эта теорема позволяет написать выражение длины вектора через его компоненты (координаты) в ортонормированном базисе.
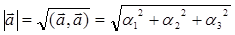 (4)
(4)
И выражение угла между векторами через их компоненты в ортонормированном базисе.
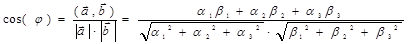 (5)
(5)
Определение: Декартова система координат, базис которой ортонормирован, называется декартовой прямоугольной системой координат.
Ортонормированный базис декартовой прямоугольной системы в трёхмерном линейном пространстве геометрических векторов обозначается обычно i, j, k. Оси координат обозначают OX, OY, OZ и называют соответственно ось абсцисс, ось ординат, и ось аппликат (см. рис  . 19). Прямоугольные декартовы координаты векторов и точек обозначают буквами x, y, z (В отличии от произвольных декартовых координат)
. 19). Прямоугольные декартовы координаты векторов и точек обозначают буквами x, y, z (В отличии от произвольных декартовых координат)
a = {x, y, z} и M(x, y, z)
 Декартовы прямоугольные координаты очень широко применяются в задачах, связанных со скалярным произведением. Легко проверить (самостоятельно), что координаты точки в декартовой прямоугольной системе равны по абсолютной величине расстояниям до соответствующих координатных плоскостей. Они имеют знак “+” или “–” в зависимости от того, лежит ли точка и базисный вектор, перпендикулярный этой плоскости, по одну сторону или по разные стороны от этой плоскости. На плоскости все аналогично, но более наглядно. Рассмотрим подробнее. (Рис 20)
Декартовы прямоугольные координаты очень широко применяются в задачах, связанных со скалярным произведением. Легко проверить (самостоятельно), что координаты точки в декартовой прямоугольной системе равны по абсолютной величине расстояниям до соответствующих координатных плоскостей. Они имеют знак “+” или “–” в зависимости от того, лежит ли точка и базисный вектор, перпендикулярный этой плоскости, по одну сторону или по разные стороны от этой плоскости. На плоскости все аналогично, но более наглядно. Рассмотрим подробнее. (Рис 20)
Пусть M(x, y) – точка на плоскости. Её радиус вектор OM = {x, y},
Т.е. OM = xi+yj. С другой стороны OM = OMx + OMy
Отсюда xi=OMx è x = ± |OMx| / |i| = ± |OMx|
(“+” – если OMx и i направлены одинаково, “–” – если в противоположенные стороны).
Аналогично y = ± |OMy|, но OMx= |OM| Cos(α) = пр ox OM,
Т.е x = |OM| Cos(α) = пр ox OM.
Аналогично OMy = |OM| cos(β) = пр oy OM,
Т.е. y = |OM| Cos(β) = пр oy OM.
Углы α и β называются направляющими углами вектора OM, а их косинусы – направляющими косинусами. Из выше сказанного следует:
Cos(α) = x / |OM|; Cos(β) = y / |OM|
Формулы для направляющих косинусов остаются в силе и в пространстве и для произвольно расположенного вектора a = {x, y, z}:
Cos(α) = x / |OM|; Cos(β) = y / |OM| Cos(g) = z / |OM|
Из формулы (4.8) следует, что расстояние между двумя точками A (x1, y1, z1) и B(x2, y2, z2) в декартовой прямоугольной системе вычисляется по формуле: 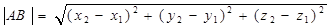
§10. Евклидово пространство.
Рассмотрим снова произвольное линейное пространство Z. В нем мы тоже можем рассмотреть понятие скалярного произведения двух векторов, а исходя из него определить важные понятия длины вектора и угла между ними (Заметим, что в обычном пространстве векторов мы поступали наоборот, хотя можно и так как будет показано ниже).
Рассмотрим только вещественные линейные пространства Z.
Определение: Вещественное линейное пространство называется Евклидовым, если в нем определена операция скалярного умножения: любым двум векторам x и y сопоставимо вещественное число (x,y) и это соответствие удовлетворяет следующим условиям: каковы бы ни были вектора x, y, z и число α.
1) (x, y) = (y, x)
2) (x+y, z) = (x, z) + (y, z)
3) (αx, y) = α(x, y)
4) (x, x)>0, если x¹0.
Следствия:
1) (x, αy) = (αy, x) = α(y, x) => (x, αy) = α (x,y)
2) (x, y+z) = (x, y) + (x, z) доказывается аналогично.
Понятие длины и угла в Евклидовом пространстве.
Определение: Длиной вектора x называется число 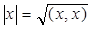
Углом между векторами x и y называется каждое число j, удовлетворяющее условию: 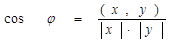
В силу аксиомы 4) длина вектора есть действительное неотрицательное число. Длина вектора равна 0 тогда и только тогда, когда вектор нулевой.
Покажем, что определение угла тоже корректно, для чего покажем, что 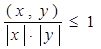 . Это будет сразу следовать из неравенства Коши-Буняковского:
. Это будет сразу следовать из неравенства Коши-Буняковского:
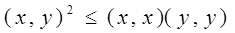 (*)
(*)
Докажем это неравенство. При любых x, y и любых числах a и b имеем:
(αx + by, αx + by) = α2(x,x)+2αb(x,y)+b2(y,y) ³ 0
Причем равенство нулю достигается тогда и только тогда, когда αx+by=0.
Пусть α= (y, y), b= - (x, y) мы получим:
(y, y)[(x,x)(y,y)-(x,y)2] ³ 0 => (*) при y¹0.
При y=0 (*) очевидна.
Из формулы (*) следует ещё одно простое и полезное неравенство:
| x+y| £ |x|+|y| (**)
На самом деле:
(x+y, x+y) = |x|2+2(x,y)+|y|2 £ |x|2+2|x| |y|+|y|2 = (|x|+|y|)2
Неравенство (**) называется неравенством треугольника:
Знак = имеет место лишь при (x,y) = |x| |y|
Сторона треугольника меньше суммы двух других сторон.
Т.е. при cos j = 1, т.е. при j=0.
Аналогично векторы называются ортогональными, если (x,y)=0
Систему векторов f1, f2, … , fm в евклидовом пространстве называют ортонормированной, если (fi, fj)=0 при i¹j и (fi, fi)=1 для любых номеров i и j.
Теорема: Ортонормированная система векторов линейно независима.
Доказательство: f1, … , fm - ортонормированная система векторов.
Рассмотрим равенство α1f1+…+α1fm = 0.
Оно возможно лишь при αi=0 (i = 1,…,m). Умножим равенство на fi. Тогда αi(fi, fi)=0 => αi=0, i – любые. => только тривиальная линейная комбинация равна 0 => Мы имеем независимую систему векторов.
Что и требовалось доказать.
Теорема: в n – мерном евклидовом пространстве существует ортонормированная система из n векторов.
Согласно предыдущей теореме такая система является базисом (его называют ортонормированным базисом).
Если e1, e2, … , en базис в Rn (иногда обозначают En), то любые векторы x и y можно записать:
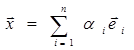
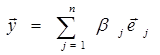
Тогда
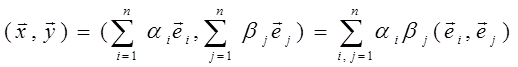
Если базис ортонормированный, то (ei,ej)=0 при i¹j и (ei,ei)=1 =>
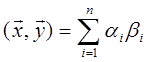
Видим, что все основные формулы обычного пространства векторов R3 обобщаются на произвольные евклидовы пространства n-ной размерности (особенно с ортонормированным базисом).
§11. Векторное произведение двух векторов.
Рассмотрим снова обычное векторное пространство геометрических векторов R (его размерность равна 3). В нем рассмотрим некоторую декартову систему координат O, e1, e2, e3, причем для определенности считаем ее правой, т.е. такой в которой кратчайший поворот первого вектора ко второму, если смотреть с конца третьего, осуществляется против хода часовой стрелки (если по часовой, то тройка будет левая). Заметим, что так определяется правая и левая тройки для любых трех некомпланарных векторов.
1) Определение векторного произведения и его основные свойства.
Определение: Векторным произведением двух векторов a и b называется такой третий вектор c, которой строится по следующим правилам:
1. Векторы a и b приводятся к общему началу О и вектор c откладывается от точки О перпендикулярно плоскости векторов a и b.
2. Векторы a, b, c должны составлять правую тройку.
3. Модуль вектора c равен площади параллелограмма, построенного на векторах a и b.
Обозначается векторное произведение a´b=c или [a,b]=c.
Например: если e1, e2, e3 – правый ортонормированный базис, то
e1´e2=e3, e2´e3=e1, e3´e1=e2 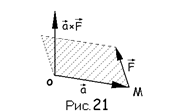
Понятие векторного произведения исходит из механики. Если вектор F изображает силу, действующую на точку М – конец вектора a = ОМ, то a´F представляет момент силы F относительно точки О (здесь вектор a - плечо)
Отметим основные свойства векторного произведения:
1. Модуль векторного произведения равен произведению модулей перемножаемых векторов на синус угла между ними. |a´b| = |a| |b| sin a (следует из определения п. 3)
2. Векторное произведение обращается в нуль тогда и только тогда, когда эти векторы коллинеарны.
Доказательство: 1) Пусть a´b=0 =>|a´b| = |a| |b| sin a = 0. Это возможно если |a| = 0 или |b| = 0 или sin a = 0. В первых двух случаях один (или два) вектора нулевые, то есть они не имеют определенного направления и их можно считать коллинеарными.
Если sin a = 0, то a = 0 или 1800 => a || b.
2) Пусть a || b => a = 0 или 1800 => sin a = 0 => |a´b| = 0 => a´b = 0
Что и требовалось доказать.
3. Свойство антиперестановочности [a, b] = - a´b 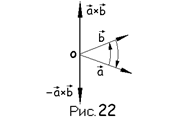
На самом деле, из определения следует, что модуль векторного произведения не зависит от порядка сомножителей, векторы a´b || b´a, но переставляя сомножители мы обязаны изменить направление произведения, чтобы тройка векторов осталась правой. Действительно, если a, b, a´b – правая, то b, a, b´a– левая, b, a, -a´b – опять правая. (см. рис 22)
4. Для любых векторов a, b и c и любых чисел l и m имеет место равенство:
(la+mb)´c =l(a´c)+m(b´c) и [a, lb´mc] = l[a, b]+m[a, c]
- распределительное свойство (без доказательства).
5. Для любых векторов a, b и любых чисел l и m имеет место равенство:
a´(lb) = l(a´b) и (la)´(mb) = (lm)(a´b)
- сочетательность относительно умножения на число (без доказательства).
2) Выражение векторного произведения через координаты перемножаемых векторов.
Пусть векторы a = {a1,a2,a3} и b = {b1,b2,b3} заданы своими координатами в базисе e1, e2, e3 . Тогда, применяя свойства 4 и 5 получим:
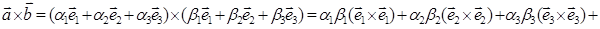
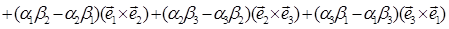
Учитывая, что в случае ортонормированного базиса i, j, k: 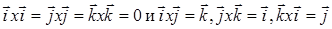
Мы получим теорему:
Теорема: В ортонормированном базисе векторное произведение выражается через координаты сомножителей в виде:
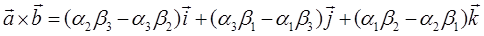
Используя определитель третьего порядка предыдущую формулу легко переписать в виде:
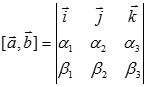
(легко видеть, раскрыв определитель по элементам первой строки)
Следствие: Если векторы a и b коллинеарны: a || b, то согласно свойству 2 a´b=0. Но это значит, что все три координаты вектора a´b обращаются в нуль:
a1b2 – a2b1=0
a2b3 – a3b2=0 или 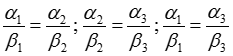 =>
=> 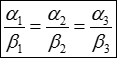
a3b1 – a1b3=0
Итак: Условием коллинеарности двух векторов является пропорциональность их координат.
3) Вычисление площади треугольника.
Из определения векторного произведения векторов a и b следует, что площадь параллелограмма, построенного на них: S = |a´b|.
Тогда площадь треугольника, стороны которого есть вектора a и b:
S треуг =|a´b| / 2.
§12. Смешанное произведение трех векторов.
Основные свойства.
Пусть даны три вектора a, b, c.
Определение: Число, получаемое от векторного произведения двух векторов и последующего скалярного умножения результата на третий, называется смешанным произведением трех векторов (иногда векторно-скалярным произведением).
Обозначается: a×(b´c), (a, [b, c]) или (a, b, c).
Отметим основные свойства смешанного произведения.
1) Свойство: Смешанное произведение трех некомпланарных векторов по модулю равно объему параллепипеда, построенного на сомножителях. Оно положительно, если вектора образуют правую тройку, отрицательно, если они образуют левую тройку.
|(a,b,c)| = |a|×|b|×|c|×sin j ×|cos q|
Vпар = Sосн × H = |b|×|c|sin j ×|a|cos q
a×[b,c] = |a|×|b´c| cos q = |a|×|b|×|c|×sin j cos q, sin j³0, 0£j£p
Поэтому знак смешанного произведения совпадает со знаком cos q => Смешанное произведение > 0, если 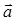 направлен в ту же сторону от плоскости векторов
направлен в ту же сторону от плоскости векторов  , что и
, что и 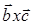 и < 0, если - в противоположную. Поэтому (a,b,c)>0 – если тройка векторов правая,
и < 0, если - в противоположную. Поэтому (a,b,c)>0 – если тройка векторов правая, 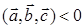 - если левая.
- если левая.
Очевидно, если e1,e2,e3 ортонормированный базис, то (e1,e2,e3)=±1 в зависимости от того, какую тройку (правую или левую) они образуют.
2) Свойство: Смешанное произведение равно нулю тогда и только тогда, когда сомножители компланарны.
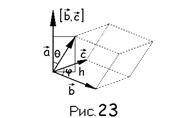 Доказательство: (a,b,c)=0 или |a|×|b|×|c|×sin j cos q = 0 возможно, если:
Доказательство: (a,b,c)=0 или |a|×|b|×|c|×sin j cos q = 0 возможно, если:
1. хоть один вектор нулевой => все 3 компланарны.
2. sin j = 0 => b||c => a,b,c компланарны
3. cos q = 0 => a перпендикулярен [b´c] => a в плоскости векторов b,c => они компланарны
Обратно: a,b,c компланарны => cos q = 0, (a,b,c)=0
3) Свойство: a×[b,c]=[a,b]×c или a×(b´c)=(a´b)×c
В самом деле. Если a,b,c правая, то a×(b´c)=Vпар, но (a´b)×c = c×(a´b)и тройка c,a,b тоже будет правой (см. чертёж) => c×(a´b) равно тому же Vпар с тем же знаком.
| “´” и “×” можно менять местами |
Поэтому часто их не ставят: abc
4) Свойство: (la1+ma2, b, c)= l(a1, b, c) + m(a2, b, c) = и аналогичные равенства для других сомножителей (без доказательства)
Выражение смешанного произведения через координаты сомножителей.
Теорема: Смешанное произведение векторов:
a = {a1, a2, a3}; b = {b1, b2, b3}; c = {g1, g2, g3 }
выражается через их координаты в произвольном базисе e1, e2, e3 в следующем виде:
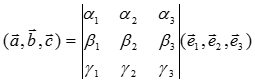 (1)
(1)
Доказательство: Согласно (1.10)
[b,c]=(b2g3 - b3g2)(e2´e3)+(b3g1 - b1g3)(e3´e1)+(b1g2 - b2g1)(e1´e2)
Умножаем скалярно обе части этого равенства на a=a1e1+a2e2+a3e3
Получим, учитывая свойства смешанного произведения
e2(e3´e1) = - e2(e1´e3) = e1(e2´e3) = (e1,e2,e3)
e3(e1´e2) = (e1´e2)e3 :
(a,b,c) = a [b,c] = a1 [b2g3 - b3g2] (e1,e2,e3) + a2 [b3g1 - b1g3] (e1,e2,e3) +
+ a3 [b1g2 - b2g1] (e1,e2,e3) =
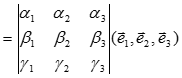
Что и требовалось доказать.
Следствие 1. Перестановка любых двух сомножителей в смешанном произведении изменяет его знак на противоположенный.
В самом деле, перестановка двух сомножителей в смешанном произведении приведет к перестановке двух строк в определителе в (1), а это изменит знак определителя (а значит и всего выражения) на противоположенный.
Итак, (a,b,c) = - (b,a,c) = (c,a,b) = - (c,b,a) = …
Следствие 2.
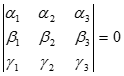
- условие компланарности векторов a,b,c
В самом деле, (a,b,c) = 0 для компланарных векторов. Но (e1,e2,e3)¹0, т. к. они образуют базис. Остается равенство нулю определителя в (1)
Следствие 3. Объем параллепипеда, построенного на векторах a,b,c (приведенных в одно начало) как на сторонах находят по формуле:
V = ± (a,b,c) (“+” – берут если тройка векторов правая, “–” – если левая)
Если базис ортонормирован (i,j,k), то
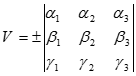 , т.к. (i,j,k) = 1
, т.к. (i,j,k) = 1
Прямая линия и плоскость
§1. Понятие уравнения линии и поверхности.
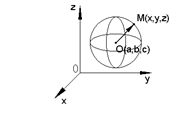 Начнем с примера. Пусть в трехмерном пространстве задана прямоугольная декартова система координат. Пусть имеется сфера радиусом R, с центром O(a,b,c).
Начнем с примера. Пусть в трехмерном пространстве задана прямоугольная декартова система координат. Пусть имеется сфера радиусом R, с центром O(a,b,c).
Обозначим точкой M(x,y,z) произвольную точку сферы. x,y,z – называются текущими координатами.
Тогда |OM| = R или 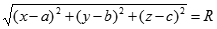 (1)
(1)
Или 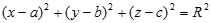 (2)
(2)
- уравнение сферы радиуса R с центром (a,b,c)
Соотношение (1) возможно для любых точек M(x,y,z) сферы и только для них => (1) есть уравнение сферической поверхности.
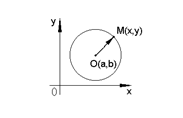 Аналогично уравнение окружности радиусом R с центром O(a,b) на плоскости будет:
Аналогично уравнение окружности радиусом R с центром O(a,b) на плоскости будет:
 (3)
(3)
- это уравнение окружности (линии на плоскости).
*) В дальнейшем под поверхностью понимаем границу некоторого тела (под линией на плоскости – границу некоторой фигуры на этой плоскости).
Определение: Равенство F(x,y,z)=0 называется уравнением поверхности в заданной системе координат, если координаты любой точки этой поверхности удовлетворяют этому уравнению. И координаты ни одной точки не лежащей на ней, ему не удовлетворяют.
Аналогично F(x,y)=0 называется уравнением линии (при тех же условиях).
Если система координат выбрана, то любая поверхность имеет определенное уравнение. Для его составления выражают геометрическое определение поверхности через координаты произвольной точки поверхности (через текущие координаты).
Очевидно, одна поверхность (линия) имеет другое уравнение в другой системе координат. Следует заметить, что иногда уравнение может определять поверхность (линию) не соответствующую нашему интуитивному понятию о них. Так x2+y2+z2 = 0 определяет поверхность из одной точки с координатами (0,0,0), а уравнение (x–1)2+(y–1)2 = 0 определяет точку с координатами (1,1) на плоскости или прямую параллельную оси Oz в пространстве, проходящую через точки с координатами (1,1,0).
Два уравнения поверхности (линии) называются эквивалентными, если одно следует из другого и наоборот. В заданной системе два уравнения определяют одну и ту же поверхность (линию) тогда и только тогда, когда они эквивалентны. Так уравнения (1) и (2) эквивалентны => определяют одну и ту же сферу.
Довольно часто линии и поверхности на плоскости и в пространстве задаются в параметрической форме.
Дата добавления: 2015-10-05; просмотров: 852;
