Выбор аппроксимирующего распределения.

Часто исследователь не имеет возможности вследствие недо­статочной изученности явления сделать выбор статистической модели для описания результатов наблюдений на основе теоретических соображений. В этом случае он осуще­ствляет выбор аппроксимирующего распределения эмпирическим путем с последующей проверкой адекватности выбранной модели реальному явлению.

Эмпириче­скими распределениями широко пользуются при моделировании функцио­нирования различного рода сложных систем методом Монте-Карло, а также при прогнозировании возможных исхо­дов в последующих опытах на основе имеющейся информации. Существует несколько методов аппроксимации эмпирических распределений.

Метод выбора и оценки параметров аппроксимирующего распределения Пирсона. Для выбора вида аппроксимирующей функции Пирсон пред­ложил использовать график, на котором по оси абсцисс отложено значение квадрата коэффициента асимметрии 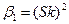, а по оси ординат - значение коэффициента эксцесса .

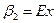На рисунке показано, как размещаются в указанной системе координат распределения: нормальное, равномерное, экспоненциаль­ное (представленные точками, так как они не имеют параметра формы), логарифмически нормальное, гамма-распределение, бета-рас­пределение Стьюдента (представленные кривыми, поскольку у них имеется один параметр формы), бета-распределение (имеющее два параметра формы и занимающее определен­ную область).

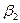Для выбора графика аппроксимирующей функции распределения необходимо знать значения и , которые, как правило, не известны и заменяются оценкам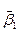и , и 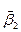, полученными на основе экспериментальных данных.

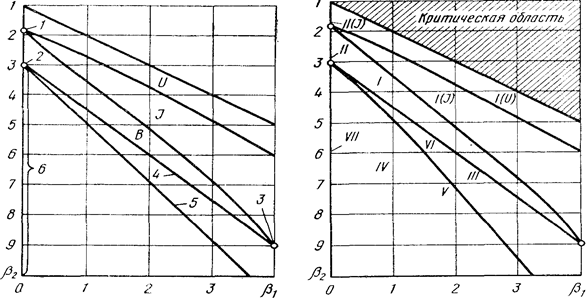
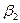Рис.11.1- Области, соответствующие различным распределениям в системе координат и области, соответствующие раз­личным распределениям Пирсона в си­стеме координат и где 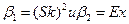: 1 - равномерное распределение; 2 - нормальное распределение: 3 - экспо­ненциальное распределение; 4- гамма-распределение: 5 - логарифмически нормальное распределение; 6 - t-рас­пределение: U-образное бета-рас­пределение: J-образное бета-рас­пределение; B-бета-распределение

Необходимые для получения оценок 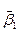, и 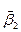центральные моменты рассчитывают по формулам:

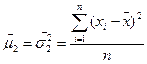,(11.1); 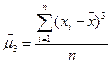,(11.2); 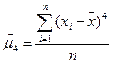,(11.3)

откуда: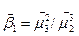 ,(11.4); 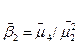,(11.5)

Значения случайных величин 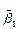, и 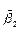очень чувствительны к отклонению отдельных крайних точек случайной величины х от ее среднего. Поэтому при малых выборках (объемом меньше 200 единиц) использование этих оценок требует большой осто­рожности.

Пирсон предложил семь типов распределений, позволяющих описывать большую область изменени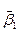й , и 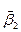, чем это удается сделать с помощью описанных выше распределений. Плотность вероятности f(x) в этих распределениях является решением дифференциального уравнения

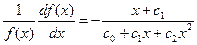; (11.6)

где началом отсчета для х служит среднее значение. Вид решения зависит от постоянных величин c₀, с₁ и c₂, которые связаны простыми соотношениями с моментами соответствующего распреде­ления вероятностей:

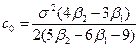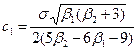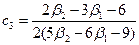; ; ; (11.7)

В качестве частных решений уравнения получаются рас­смотренные выше нормальное распределение бета-распределение (распределение Пирсона типа I) и гамма-распределение (рас­пределение Пирсона типа III).

Распределения Пирсона типа II симметричны относительно центральной ординаты и имеют конечный размах, типа IV асим­метричны с неограниченным в обоих направлениях размахом, типа V асимметричны с ограниченным с одной стороны размахом (0<= х < 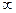), типа VI асимметричны с ограниченным с левой сто­роны размахом (a < х < 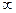), типа VII симметричны относительно оси ординат с неограниченным размахом в обе стороны. Частным случаем этого типа распределения является нормальное распре­деление.

Область точек ( 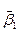, 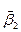) которым соответствуют определенные кривые распределений, ограничена сверху и снизу прямыми, описываемыми соответственно уравнениям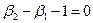и: и 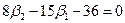(11.8)

Более подробно с распределениями Пирсона и методами под­бора аппроксимирующих кривых можно познакомиться в литературе.