Нормальный закон распределения. Рассмотрим проверку предположения о нормальном законе рас­пределения случайной величины на примере

Рассмотрим проверку предположения о нормальном законе рас­пределения случайной величины на примере. Данные проранжированы и в последней колонке приведены накопленные значения, по которым рассчитаны оценки 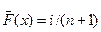приведенные в табл. 11.1. Приравнивая F(u) значению 0,0175 и учитывая, что значение u_0,0175 = - u_0,9825 находим по обрат­ной функции нормального распределения значение u_0,0175 = -2,11, соответствующее нижнему концу шкалы значений u. Аналогично этому, приравняв F(u) значению 0,983, находим u_0,983 = 2,12. Принимаем пределы изменения u равными -2,5

В результате получаем расположение точек, через которое трудно провести прямую. Это дает основание предпола­гать, что значения случайной величины не имеют нормального распределения.