Пропорциональность дисперсии у известной функции от х

Если величина условной дисперсии Dy/x пропорциональна некоторой известной функции h²(х), т. е. если

Dy/x = 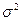h²(х) ; (12.37)

то значение параметров в уравнении регрессии определяют, ми­нимизируя нормированную сумму квадратов отклонений экспе­риментальных данных от эмпирической линии регрессии:

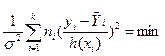; (12.38)

Обозначив 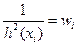, получим методом наименьших квадратов

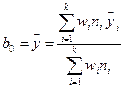; (12.39)

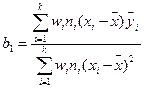; (12.40)

где

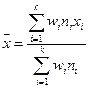; (12.41)

Проверку гипотезы о линейности связи осуществляют, сопо­ставляя дисперсии средних 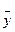, относительно линии регрессии

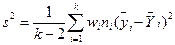; (12.42)

с дисперсией индивидуальных значений 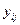относительно средних :

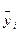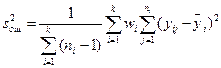(12.43)

Если отношение F = s²/s²_ош меньше табличного значения F для заданного уровня значимости а при числе степеней свободы для числителя f = k - 2 и для знаменателя f = N - k, то рассчи­тывают оценку остаточной дисперсии

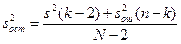; (12.44)

Оценка значимости b₀ осуществляется путем расчета отношения

; (12.45)

где: 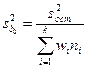; (12.46)

Оценку значимости b₁ делают, рассчитывая отношение

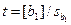; (12.47)

где: 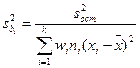; (12.48)

Отношения, рассчитанные по уравнениям (266) и (268), сопоставляют с табличными значениями t для заданного уровня зна­чимости a и при числе степеней свободы f = N – 2.