Линейный регрессионный анализ с двумя независимыми переменными
Cлучайная величина y является линейной функцией от переменных x1 и x2
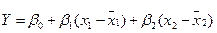; (12.53)
Как и в случае с одной независимой переменной, предполагается, что для каждого фиксированного значения (x1 , x2) величина у нормально распределена, дисперсия не зависит от (x1, x2), пропорциональна известной функции (x1, x2), т.е.: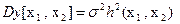 
(12.54)
Предполагается также, что наблюдения стохастически независимы , т.е.
(x1i, x2i, yi) независимы от (x1j, x2j, yj)
Кроме этих предпосылок регрессионного анализа, появляется еще одна предпосылка - требование линейной независимости переменных (x1, x2)
Пусть в результате эксперимента получено n групп чисел (x1i, x2i, yi) где i = 1, 2, . . .,n Результаты наблюдений не образуют групп при каждом значении i и дисперсия y не зависит от (x1 , x2). Нужно найти оценки параметров 
.
Оценки параметров .осуществляют методом наименьших квадратов минимизируя сумму квадратов отклонений наблюдаемых значений y от эмпирическои плоскости регрессии.
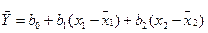; (12.55)
Берем частные производные по b0, b1, b2 от суммы квадратов отклонений
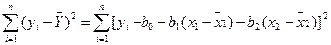. (12.56)
Приравнивая три производные нулю, получим систему из трех уравнений:
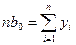; (12.57)
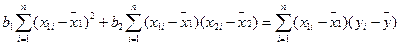; (12.58) 
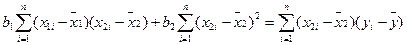; (12.59)
Решая эту систему уравнений относительно параметров b0, b1, b2 получим
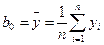; (12.60)
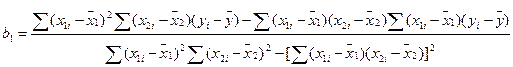; (12.61)
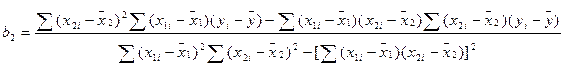; (12.62)
Из выражений видно, что оценки b0, b1, b2 представляют собой линейные функции y и в соответствии с теоремой сложения для нормального распределения они распределены нормально с дисперсиями:
; (12.63)
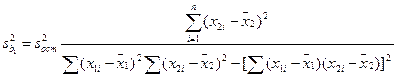; (12.64)
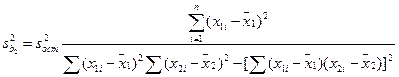; (12.65)
Смешанный второй момент или ковариация коэффициентов регрессии b1, b2 равна: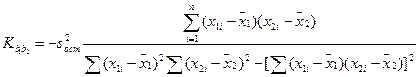 
; (12.66)
Величина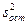 
представляет собой дисперсию экспериментальных точек относительно эмпирической поверхности регрессии - так называемую остаточную дисперсию:
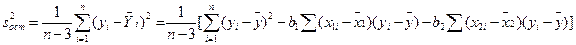; (12.67)
Значимость найденных оценок b0, b1, b2 проверяют, рассчитывая отношения:
(12.68) ;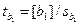 
(12.69); 
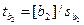; (12.70)
которые сопоставляют с табличными значениями t для заданного а при числе степеней свободы: f = n-3
Проверк:у гипотезы о линейности связи осуществляют путем расчета отношения дисперсии экспериментальных значений y обусловленной регрессией y на x1 и x2, равной
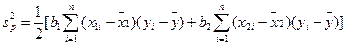; (12.71)
к остаточной дисперсии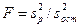 
Величину отношения F сравнивают с табличным значением при заданном а и числе степеней свободы fp =2 и f = n -3. если F равна или больше табличного, то гипотеза о линейности связи не противоречит экспериментальным данным.
Уравнение регрессии характеризуется совокупным коэффициентом детерминации:
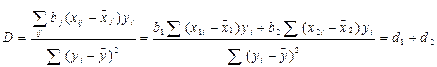; (12.72)
Чтобы определить с максимальной точностью положение в пространстве поверхности регрессии, необходимо не только варьировать значения независимых переменных x1, x2 по возможности в более широких пределах, но и добиваться независимо друг от друга их изменения. При несоблюдении последнего условия значения угловых коэффициентов b1, b2 искажаются и в результате рассмотрения можно прийти к ошибочным выводам о влиянии рассматриваемых факторов x1, x2 на y.
Часто для более детального изучения связи между x1, x2 и y применяют последовательный регрессионный анализ определяя влияние каждого фактора отдельно:
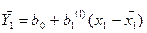(12.73)
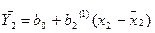(12.74)
и затем расчитыают уравнение:
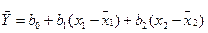(12.75)
Для выяснения вопроса о целесообразености включения в модель того или иного члена делают оценку эффекта от включения его в модель с помощью F критерия.
При сильной корреляции между x1, x2 интерпретация уравнения регрессии затруднена, а применение методов ортогонолизации переменных еще более затрудняет оценку. В некоторых случаях, когда переменные x2 иy закономерно изменяются с изменением x1 – достаточно эффективен метод каскадного анализа –регрессионный анализ с заменой наблюдаемых величин расчетной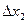 
:
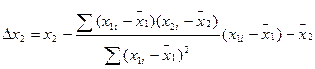; (12.76)
Расчетная величина 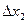ортогональна по отношению к x1 , при наличии линейной связи между x1 и x2. Благодаря этому коэффициенты регрессии в уравнении некореллированы.
Контрольные вопросы:
1.Сущность регрессионного анализа с одной переменной.
2.Методы регрессионного анализа с двумя независимыми переменными.
3.Что называют множественным регрессионным анализом.
Дата добавления: 2015-10-05; просмотров: 1031;