Статистическая проверка гипотез
Статистическими гипотезами называют предположения относительно закона распределения F(х) рассматриваемой величины и, о параметрах этого распределения. Правильность гипотез проверяется путем вычисления некоторых числовых характеристик по данным наблюдений и сравнения их с теми, которые должны быть при условии, что проверяемая гипотеза Н0 истинна, а наблюдаемые отклонения объясняются случайными колебаниями в выборках. Такие характеристики называют критериями проверки статистической гипотезы. Они представляют собой случайные величины, значения которых определяются выборкой. Гипотезу считают правильной, если значение рассчитанного критерия не выходит за границы значимости. Эти границы устанавливают по таблицам в соответствии с уровнем значимости, которому должна соответствовать вероятность ошибки 1-го рода - забраковать проверяемую гипотезу, когда она верна.
Обычно пользуются тремя уровнями значимости a: 0,05, 0,01 и 0,001 или соответствующими им тремя Q-процентными точками (Q = 100 a: 5, 1 и 0,1%). Поскольку a = 1 - q, то критические значения рассматриваемой случайной величины можно определять также по таблицам квантилей учитывая, что
xa = xq-1-a
C уменьшением уровня значимости увеличивается вероятность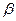 
совершить ошибку 2-го рода - принять гипотезу, когда она неверна, а справедлива альтернативная гипотеза Н1.
Области принятия нулевой гипотезы Н0 и ее отклонения (критической области) выбирают, пользуясь величиной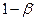 
, именуемой мощностью критерия.
Для оценки гипотез относительно отдельных параметров распределения: среднее, дисперсия, коэффициент корреляции и т.д.- применяют критерии значимости. К числу наиболее часто используемых критериев относятся критерий t- Стьюдента, критерий F- Фишера, критерий 
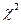- Пирсона и ряд других. Использование этих характеристик в качестве критериев основано на знании точных законов их распределения в том случае, когда случайная величина Х имеет нормальный закон распределения.
1. Проверка гипотез о законе распределения случайной величины
Существует много критериев для оценки предположения о законе распределения случайной величины. Наиболее часто применяемый критерий согласия 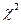-Пирсона, позволяет оценить подобие между эмпирическим распределением величины х и его моделью при любом законе распределения. Этот критерий не является безупречным, его недостатки заключаются в нечувствительности к обнаружению адекватной модели при небольшом числе наблюдений (N < 100), а также в зависимости значения критерия 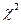от величины и положения интервалов группировки. Проверку согласия между теоретической функцией распределения и эмпирическим распределением осуществляют в последовательности:
1. Рассчитывают по выборке данных оценки математического ожидания
Мх = 
и дисперсии s2.
2. Ранжируют случайную величину х по возрастающему ее значению
x1 <= x2 <= x3 <=…<=xN
3. Область изменения случайной величины разбивают на k интервалов. Число интервалов выбирают произвольно. Желательно, чтобы математическое ожидание числа наблюдений Mni, в i-том интервале распределения согласно принятой модели и оценок параметров, было >=10; но не менее 5. Число интервалов k не рекомендуется делать более 25, так как это увеличивает объем вычислений, но не повышает чувствительности критерия.
Разбивку на интервалы осуществляют двумя способами. Если исходные данные были уже сгруппированы по интервалам до проверки согласия или если имеет место дискретное распределение, например распределение Пуассона, то сохраняют первоначальную группировку при условии, что она удовлетворяет требованиям п. 3. Если в каком-либо интервале ожидаемое число наблюдений Mni меньше 5, то этот интервал объединяют с соседним.
При непрерывных распределениях, когда исходные данные предварительно не сгруппированы, границы интервалов определяют с помощью теоретического распределения и полученных в п.1 оценок его параметров таким образом, чтобы вероятность попадания случайной величины в каждый интервал равнялась 1/k. В соответствии с этим верхние границы интервалов хi, определяют из равенств
р (х <= х1) = 1/k, р (х <= х2) = 2/k, . . ., р (х <= хk-1) = (k-1)/k (11.9)
Cпособ группировки данных позволяет получить свободный от второго из недостатков критерий .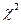
4.Вероятность попадания случайной величины в i-тый интервал при первом способе группировки наблюдений оценивают следующим образом:
а) Определяют величину нормированного отклонения переменной величины, соответствующей верхней границе l-го интервала, от средней по выборке:
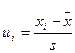; (11.10)
б) По таблицам нормированной функции нормального распределения определяют Ф (ui), и рассчитывают: pi = Ф (ui) - Ф (ui-1) ; (11.11)
5. Умножая вероятность попадания в i-тый интервал на объем выборки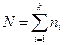 
, получают математическое ожидание Mni, числа наблюдений в i-том интервале.
6. Рассчитывают квадрат величины отклонения числа наблюдений в каждом интервале от соответствующего математического ожидания и делят полученную величину на математическое ожидание.
7. Вычисляют критерий: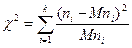 
(11.12)
При разбивке области изменения x на интервалы с одинаковым значением математического ожидания: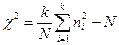 
(11.13)
8. Сравнивают вычисленное значение 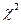с табличным, для заданного уровня значимости a и числа степеней свободы f = k- r - 1
где r- число параметров, оценки которых получены на основе наблюдений. Если расчетное значение 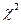превышает табличное, то модель распределения отвергается, в ином случае считают, что она не противоречит наблюдениям.
2. Графический метод оценки распределения экспериментальных данных
Соответствие распределения экспериментальных данных закону распределения можно приближенно оценить, построив график, по оси абсцисс которого отложить значения случайной величины, а по оси ординат - значения интегральной функции распределения, принятого в качестве модели.
Построение графика осуществляют в следующей последовательности.
1. Ранжируют случайную величину по возрастающему ее значению и рассчитывают значение накопленной (кумулятивной) частоты эмпирического распределения. При расчете накопленных частот часто используют оценку:
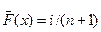; (11.14)
где i- число данных, у которых х <= xi ; n - число испытаний.
Эта оценка применима и в случае неограниченных распределений.
2. Приравнивая интегральную функцию теоретического распределения минимальному и максимальному значениям накопленной частоты, определяют пределы отклонения величины от нуля, и на этой основе определяют масштаб для нанесения вспомогательной шкалы значений и на оси ординат.
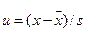; (11.15)
Она служит для построения шкалы интегральной функции распределения, выбранной в качестве модели. Обычно шкалу наносят справа от графика.
3. По таблицам нормированных распределений находят квантили и, соответствующие различным значениям интегральной функции распределения, и через них проводят прямые, параллельные оси абсцисс, которые образуют масштабную сетку вероятности p(u <= a) = F(а).
Для различных распределений эта сетка имеет различный вид.
4. Наносят на график значения накопленной частоты против соответствующих значений случайной величины. Если вид функции распределения выбран правильно, то экспериментальные точки должны ложиться на прямую.
Дата добавления: 2015-10-05; просмотров: 574;