Оценка параметров нормального распределения по экспериментальным данным
Оценку математического ожидания vx вычисляют по формуле
vx = 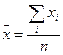 (10.7)
(10.7)
где хi - значение i-того результата определения х; n - число испытаний.
Здесь и дальше знак _ над обозначением того или иного параметра означает, что мы имеем дело с оценкой этого параметра.
Для дисперсии, 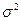 существуют две оценки:
существуют две оценки:
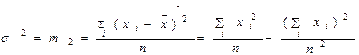 (10.8)
(10.8)

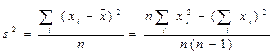 (10.9)
(10.9)
Первая оценка, являющаяся оценкой максимального правдоподобия, имеет смещение, а вторая оценка смещения не имеет, и по этой причине ею пользуются чаще. При больших значениях различие в величине этих оценок стремится к нулю. Следует отметить, что среднее квадратическое отклонение s не являете несмещенной оценкой. Таким образом, эмпирическое среднее х стремится по вероятности к центру распределения vx при n 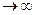 и может использоваться как оценка этого параметра.
и может использоваться как оценка этого параметра.
Контрольные вопросы:
1. Законы распределения параметров: непрерывные и дискретные распределения.
2. Закон нормального распределения, другие виды распределений случайной величины и применение.
3. Оценка параметров нормального распределения: математическое ожидание, дисперсия.
Дата добавления: 2015-10-05; просмотров: 694;
