Характеристики распределений

Математическое ожидание или среднее значение случайной величины

МХ = v_x.(9.2)

В случае непрерывной случайной величины

МХ = 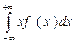(9.3)

где f(х) - плотность распределения величины х.

Если же х - дискретная случайная величина, то

МХ= 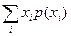(9.4)

где р(х_i) — вероятность появления i-того значения величины х.

Медиана - значение случайной величины, отвечающее сере­дине упорядоченного по величине ряда значений переменной. В случае непрерывной случайной величины медианой является такая точка z, при которой

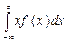= 0,5 (9.5)

а в случае дискретной переменной

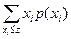=0,5. (9.6)

Если общее число n значений дискретной случайной величины нечетно, то медиана равна значению случайной величины с ин­дексом i=(n+1)/2. При четном n медиана равна

½(x_n/2 + x_(n/2+1))(9.7)

Мода - значение случайной величины, отвечающее макси­мальной плотности вероятности f(х) в случае непрерывной слу­чайной величины, или значение случайной величины, имеющей максимальную вероятность в том случае, когда случайная вели­чина дискретна.

Кроме характеристик положения центра, пользуются еще рядом других характеристик, описывающих рассеяние, симме­трию и островершинность распределения. Эти характеристики можно, представить с помощью моментов распределения. На практике чаще всего применяют моменты двух видов: начальные и центральные.

Начальным моментом s-ного порядка дискретной случайной величины Х называют сумму вида: v_s= 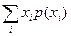(9.8)

а в случае непрерывной случайной величины он равен

v_s= 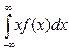(9.9)

Таким образом, начальный момент s-ного порядка есть мате­матическое ожидание s-ной степени случайной величины X:

v_s = МХ^s.(9.10)

Начальный момент первого порядка случайной величины Х равен математическому ожиданию v_x.

Центральным моментом 5-ного порядка случайной величины Х называют математическое ожидание s-ной степени отклонения случайной величины Х от ее математического ожидания v_x

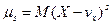(9.11)

Для дискретной случайной величины s-ный центральный момент равен

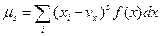(9.12)

а для непрерывной - интегралу

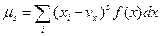(9.13)

Центральный момент второго порядка 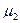- диспер­сия, служит в качестве меры рассеяния:

DX = 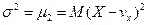(9.14)

Корень квадратный из дисперсии- средне квадратическое отклонение или стандарт.

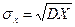(9.15)

В качестве относительной характеристики рассеяния исполь­зуют коэффициент вариации- отношение среднего квадратического отклонения к математическому ожида­нию случайной величины

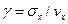(9.16)

Центральный момент третьего порядка 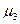используется для числового измерения асимметрии распределения. Если распреде­ление симметрично, то 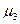= 0. Если правое плечо распреде­ления длиннее левого, то величина 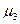положительная, если же, наоборот, левое плечо длиннее правого, то величина 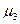отрица­тельна. Чтобы иметь дело с безразмерной величиной 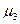делят на 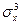. Полученный показатель называют коэффициентом асимметрии (skewness)

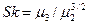(9.17)

В качестве характеристики островершинности служит коэф­фициент эксцесса (excess) 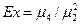(9.18)