Нахождение оценок параметров распределения

В тех случаях, когда параметры распределения случайной переменной Х неизвестны, их оценивают на основе эксперимен­тальных или статистических данных. Поскольку значения оценок зависят от вошедших в выборку значений случайной величины, постольку они являются также случайными величинами.

Оценки по возможности должны обладать свой­ствами: состоятельностью, несмещенностью и эффективностью. Оценку 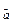называют состоятельной, если при неограниченном увеличении числа наблюдений n она стремится по вероятности к значению а. Если она при этом не дает систематической ошибки, т. е. если выполняется условие М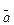= а, то такую оценку назы­вают несмещенной. Несмещенную оценку называют эффективной, если она имеет наименьшую дисперсию по сравнению с другими несмещенными оценками параметра а.

Оценки параметров распределения чаще всего находят, поль­зуясь методом моментов или методом наибольшего правдоподобия.

Метод моментов в большинстве случаев более простой и им удобно пользоваться. Он заключается в том, что искомые чис­ловые характеристики распределения выражают через моменты низших порядков, которые затем заменяют их оценками, полу­ченными по результатам наблюдений. Количество составленных таким образом уравнений должно равняться числу оцениваемых параметров распределения. Решая совместно эти уравнения, получают требуемые оценки. Применение метода иллюстрируется ниже при нахождении параметров гамма-распределения. Метод моментов иногда приводит к малоэффективным оценкам.

Метод наибольшего (максимального) правдоподобия часто тре­бует более сложных вычислений, чем метод моментов, однако лучше пользоваться им, так как он всегда приводит к состоятельным, асимптотически нормальным и асимптотически эффективным оценкам. Иногда оценки могут иметь небольшое смещение. Метод наибольшего правдоподобия предполагает принятие в качестве оценки неизвестного параметра такого его значения, появление которого на основе имеющихся данных наиболее вероятно. По методу наибольшего правдоподобия в качестве оценки параметра, от которого зависит плотность вероятности, принимают такое его значение, при котором достигает максимума функция правдоподобия.

L= f(x₁) f(x₂) …f(x_n) = П f(x_i) (9.19)

где x₁, x₂ …x_n - результаты n независимых наблюдений ис­следуемой случайной величины; f(x_i) - плотность распределения, определяемая формулой в соответствии с принятой мо­делью распределения.

Для нахождения максимума возьмем частную производную ln L по 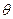и приравняем ее нулю

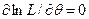(9.20)

Решая это уравнение относительно 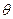, находим оценку 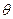мак­симального правдоподобия. Если плотность распределения определяется несколькими параметрами, то оценки находят, беря частные производные от логарифма функции правдоподобия но каждому из искомых пара­метров, приравнивая эти производные нулю и решая совместно полученные уравнения относительно параметров.

Контрольные вопросы:

1. Законы распределения параметров, характеризую­щих адекватное функционирование математической модели объекта, интегральная функция распределения.

2. Характеристики распределений, математическое ожидание и среднее значение случайной величины, плотность распределения величины.

3. Что называют начальным и центральным моментоми s-ного порядка дискретной случайной величины Х.

4. Дисперсия и средне квадратическое отклонение случайной величины.

5. Нахождение оценок параметров распределения: метод моментов, метод наибольшего (максимального) правдоподобия