МНК для парной линейной регрессии

Для оценки параметров a, b обычно применяют метод наименьших квадратов (МНК). Существуют и другие методы оценки параметров, например, метод моментов, метод наименьших модулей, метод максимального правдоподобия. Рассмотрим метод наименьших квадратов.

Если имеется n наблюдений, уравнение (1.1) можно представить в следующем виде:

y_i = a + bx_i + ε_i , i = 1, 2, 3, … , n.

Случайное отклонение ε можно рассматривать как последовательность n случайных величин ε_i , i = 1, 2, 3, … , n.

Метод наименьших квадратов позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений признака y_i от расчетных (теоретических) y_xi является минимальной:

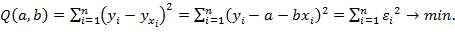(1.2)

Необходимым условием существования минимума функции двух переменных Q(a,b) (1.2) является равенство нулю ее частных производных по неизвестным параметрам a и b:

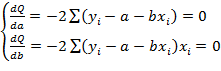
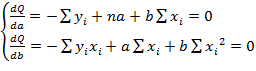(1.3)

После преобразований получаем систему уравнений:

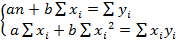(1.4)

Система уравнений (1.4) представляет собой систему нормальных уравнений МНК.

Разделив оба уравнения системы (1.4) на n, получим:

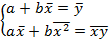
Отсюда находим a и b:

В этих уравнениях 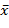и 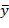- это средние значения переменных x и y.

Коэффициент b при x называется коэффициентом регрессии. Если переменную x изменить на единицу, т.е. взять за x величину x+1, то новое значение y_x(x+1) будет равно y_x(x)+b. Следовательно, коэффициент регрессии показывает среднее изменение результата y при изменении фактора x на единицу.

Коэффициент a – свободный член уравнения регрессии - указывает на значение результативного признака при нулевом значении фактора. Это важный индикатор для выбора вида уравнения регрессии. Например, если в результате вычислений коэффициент a оказался отрицательным, а экономический смысл задачи диктует положительность или равенство нулю показателя a , значит, выбор вида уравнения был неудачен.