Свойства операций сложения и умножения матриц
1.A + B = В + A
2.(A + B) + C = A + (B + C)
3.λ(A + B)=λA + λB
4.(λ+μ)A = λA+ μA
5.(λμ)A= λ(μA)
6.A  (B + C) = A
(B + C) = A  B + A
B + A  C
C
7.λ(A  B)= (λA) B = A(λB)
B)= (λA) B = A(λB)
8.A  (BC) = (AB)
(BC) = (AB)  C
C
Заметим, что умножение матриц не обладает свойством коммутативности, т.е.
AB 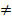 ВA
ВA
Пример 1.3.Даны две матрицы A и B. Найти их произведение AB.
А= 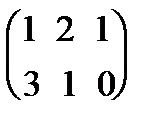 , В =
, В = 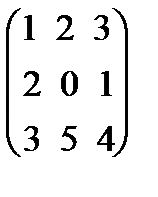 .
.
Решение. Поскольку матрица А размера 2´3, матрица В размера 3´3, то произведение АВ=С существует и элементы матрицы С равны
с11 = 1×1 +2×2 + 1×3 = 8, с21 = 3×1 + 1×2 + 0×3 = 5, с12 = 1×2 + 2×0 + 1×5 = 7,
с22 =3×2 + 1×0 + 0×5 = 6, с13 = 1×3 + 2×1 + 1×4 = 9, с23 = 3×3 + 1×1 + 0×4 = 10.
AB = 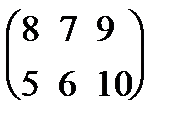 , а произведение BА не существует.
, а произведение BА не существует.
Пример 1.4.Даны две матрицы A и B. Найти их произведение AB.
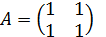 ,
, 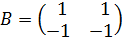 .
.
Решение.
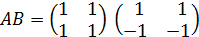 =
= 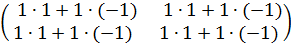 =
= 
Таким образом, произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что 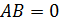 , не следует, что
, не следует, что 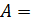 0 или
0 или 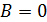 .
.
Пример 1.5. Даны две матрицы A и B. Найти: а) AB; б) BA; в) 3АВ-2А
A = 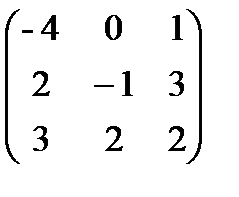 , B =
, B = 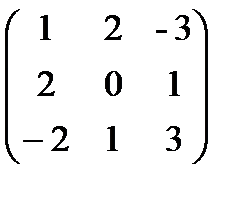 .
.
Решение. а) Произведение АВ имеет смысл, так как число столбцов матрицы А равно числу строк матрицы В. Находим матрицу С=АВ, элементы которой определяются по формуле cij =ai1b1j+. ai2b2j+ ai3b3j+. …+ ainbnj. Имеем:
AB= 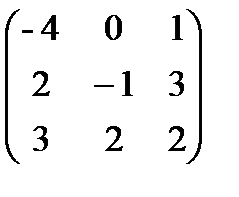
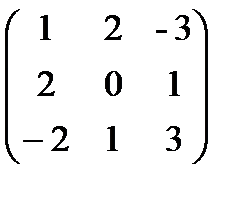 =.
=. 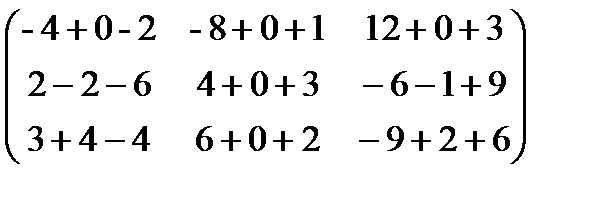 =
= 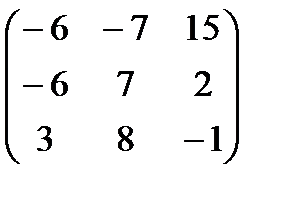
б) Вычислим BA= 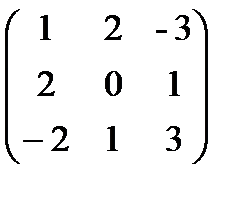 .
. 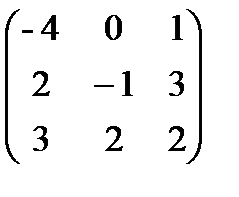 ==.
==. 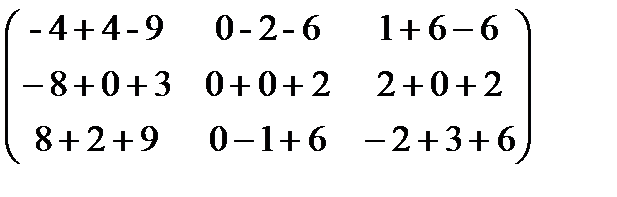 =
= 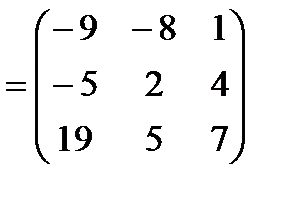
Очевидно, что AB 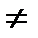 BA
BA
в) Вычислим 3АВ-2А, используя полученный результат для АВ из пункта а)
3АВ-2А = 3 
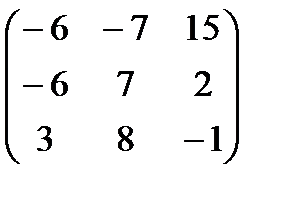 - 2
- 2 
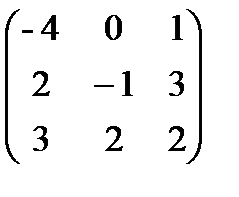 =
= 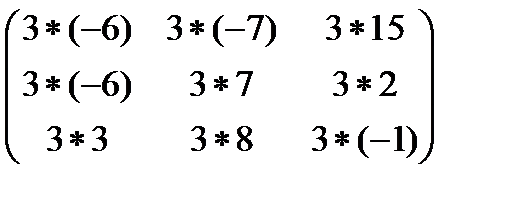 -
- 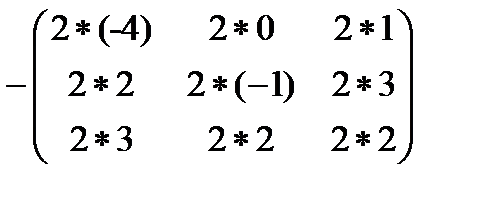 =
= 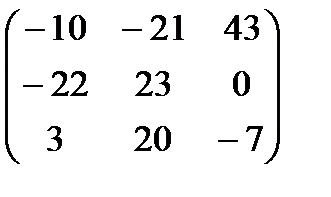
Пример 1.6.В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М1, М2 и М3, причем доставка единицы продукции с каждого молокозавода в магазин М1 стоит 50 ден. ед., в магазин М2 - 70, а в М3 - 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.
| Молокозавод | Магазин | ||
| М1 | М2 | М3 | |
Решение.Обозначим через А матрицу, данную нам в условии, а через
В - матрицу, характеризующую стоимость доставки единицы продукции в магазины, т.е.,
А = 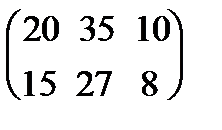 , В = (50, 70, 130).
, В = (50, 70, 130).
Тогда матрица затрат на перевозки будет иметь вид:
АВT = 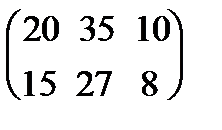
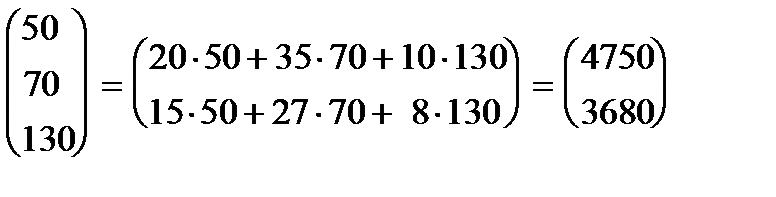 .
.
Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй - 3680 ден.ед.
Пример 1.7. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется вектором-строкой X = (10, 15, 23). Используются ткани четырех типов Т1, Т2, Т3, Т4. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Вектор-строка С = (40 35 24 16) задает стоимость метра ткани каждого типа, а вектор-строкаP = (5 3 2 2) - стоимость перевозки метра ткани каждого вида.
| Изделие | Расход ткани | |||
| Т1 | Т2 | Т3 | Т4 | |
| Зимнее пальто | ||||
| Демисезонное пальто | ||||
| Плащ |
1. Сколько метров ткани каждого типа потребуется для выполнения плана?
2. Найти стоимость ткани, расходуемой на пошив изделия каждого вида.
3. Определить стоимость всей ткани, необходимой для выполнения плана.
4. Подсчитать стоимость всей ткани с учетом ее транспортировки.
Решение.Обозначим через А матрицу, данную нам в условии, т. е.,
A = 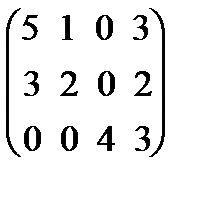 ,
,
тогда для нахождения количества метров ткани, необходимой для выполнения плана, нужно матрицу X умножить на матрицу А:
XА=(10 15 23) 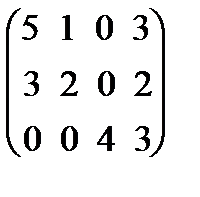 =
= 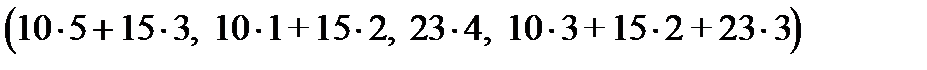 =
=
= (95 40 92 129).
Стоимость ткани, расходуемой на пошив изделия каждого вида, найдем, перемножив матрицу А и CT:
А CT = 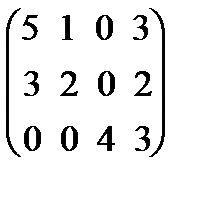
 =
= 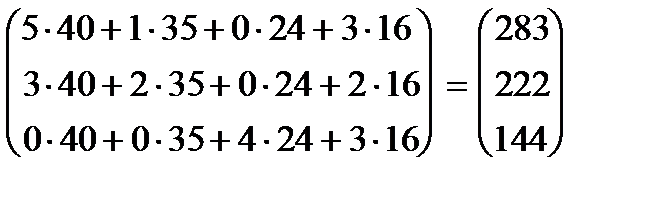 .
.
Стоимость всей ткани, необходимой для выполнения плана, определится по формуле:
XАC T = (10 15 23) 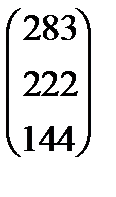 =
= 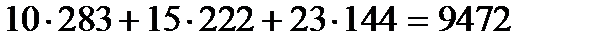 .
.
Наконец, с учетом транспортных расходов вся сумма будет равна стоимости ткани, т. е. 9472 ден. ед., плюс величина
XАP T = (95 40 92 129) 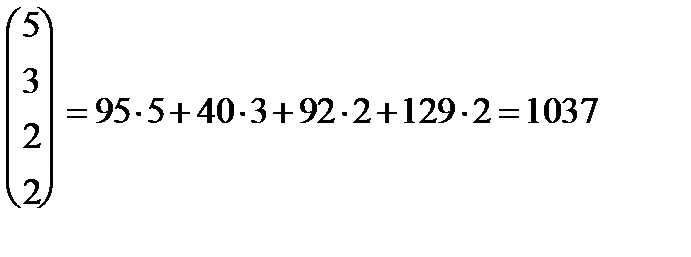 .
.
Итак, XАC T + XАP T = 9472 + 1037 = 10509 (ден. ед).
4) Возведение в степень.
Целой положительной степенью Аm (m>1) квадратной матрицы А называется произведение m матриц равных А, т.е. 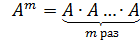 .
.
Операция возведения в степень определена только для квадратных матриц. По определению полагают
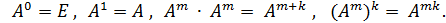
Пример 1.8. Найти B3, если 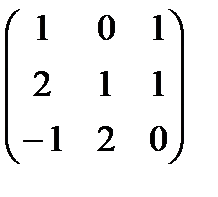
Решение. Сначала найдем В2=ВB= 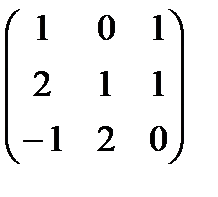
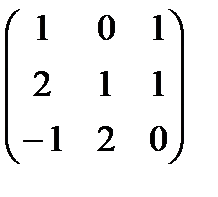 =
= 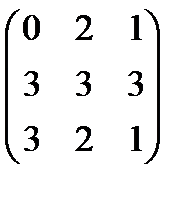 .
.
В3=ВВ2 = 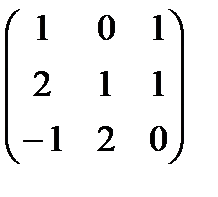
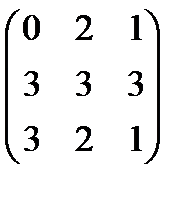 =
= 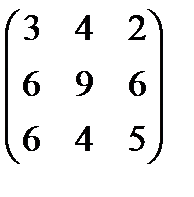 .
.
Легко убедиться, что В3=В2В = 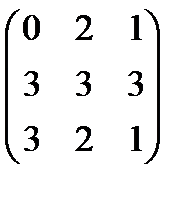
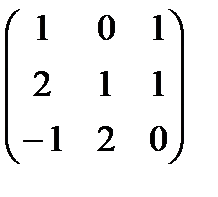 =
= 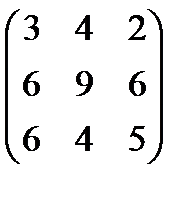 , что подтверждает правильность сочетательного закона при умножении матриц.
, что подтверждает правильность сочетательного закона при умножении матриц.
Дата добавления: 2015-09-29; просмотров: 870;
