Свойства определителей. 1. Определитель не меняется при транспонировании.
1. Определитель не меняется при транспонировании.
2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
3. Если в определителе переставить две строки, определитель поменяет знак.
4. Определитель, содержащий две одинаковые строки, равен нулю.
5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.
6. Определитель, содержащий две пропорциональные строки, равен нулю.
7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых ai j = bj + cj (j=  ), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.
), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.
8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
МиноромMij элемента aij определителя  n-го порядка называется определитель порядка n-1, который получается из
n-го порядка называется определитель порядка n-1, который получается из  вычеркиванием строки и столбца, содержащих данный элемент.
вычеркиванием строки и столбца, содержащих данный элемент.
Алгебраическим дополнением элемента aij определителя  называется его минор Mij, взятый со знаком (-1) i + j. Алгебраическое дополнение элемента aij будем обозначать Aij. Таким образом, Aij = (-1) i + j Mij.
называется его минор Mij, взятый со знаком (-1) i + j. Алгебраическое дополнение элемента aij будем обозначать Aij. Таким образом, Aij = (-1) i + j Mij.
На практике определители удобно находить, используятеорему оразложенииопределителя по строке или столбцу:
Теорема 1.1(разложение определителя по строке или столбцу).
Определитель матрицы A=( 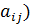 равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение определителя
равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение определителя  по элементам i-й строки
по элементам i-й строки
 = ai 1 Ai 1 + ai 2 Ai 2 +... + ai n Ai n (i =
= ai 1 Ai 1 + ai 2 Ai 2 +... + ai n Ai n (i =  )
)
или j- го столбца
 = a1 j A1 j + a2 j A2 j +... + an j An j (j =
= a1 j A1 j + a2 j A2 j +... + an j An j (j =  ).
).
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
В дальнейшем i -ую строку определителя или матрицы будем обозначать Si, а j-ый столбец - Сj.
Пример 1.10. Для данного определителя  :
:
1) найти миноры и алгебраические дополнения элементов a12 и a32.
2) Вычислить определитель : а) разложив его по элементам 1-ой строки; б) разложив его по элементам 2-го столбца; в) получив предварительно нули в 1-ой строке.
 =
= 
Решение. 1). Находим миноры к элементам a12 и a32 по правилу треугольников:
M12 = 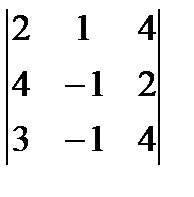 = -8-16+6+12+4-16=-18,
= -8-16+6+12+4-16=-18,
M32 = 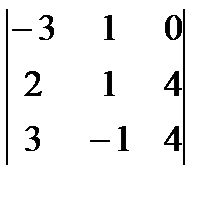 =-12+12=12-8=-20.
=-12+12=12-8=-20.
Алгебраические дополнения элементов a12 и a32 соответственно равны:
A12 =(-1)1+2 M12 –(-18)=18,
A32 =(-1)3+2 M32 –(-20)=20,
2) а). Вычислим определитель, разложив его по элементам первой строки:
 = a1 1 A11j + a12 A12 + a13 A13 + a14 A14 =-3
= a1 1 A11j + a12 A12 + a13 A13 + a14 A14 =-3 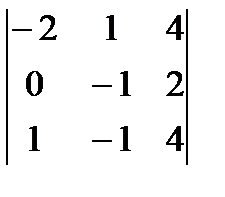 - 2
- 2 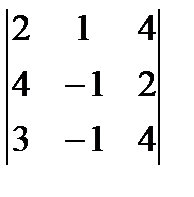 + 1
+ 1 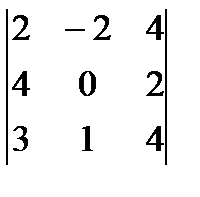 - +0
- +0 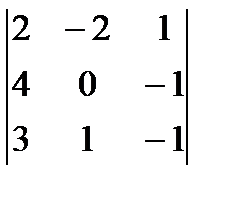 -= -3(8 + 2 + 4 – 4) - -2(-8 – 16 + 6 + 12 +4 + 16) + (16 – 12 – 4 + 32) = 38.
-= -3(8 + 2 + 4 – 4) - -2(-8 – 16 + 6 + 12 +4 + 16) + (16 – 12 – 4 + 32) = 38. 
б) Вычислим определитель, разложив его по элементам второго столбца:
 = a2 1 A21 + a22 A22 + a23 A23 + a24 A24 =-2
= a2 1 A21 + a22 A22 + a23 A23 + a24 A24 =-2 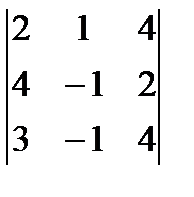 - 2
- 2 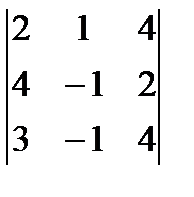 +
+
+0 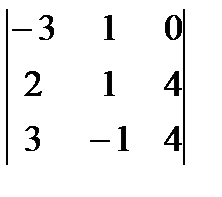 +1
+1 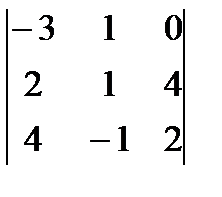 = -2(-8 + 6 - 16 +12 +4 - 16) – 2(12+ 6 – 6 – 16) + (-6 + 16 - - 12 – 4)=38.
= -2(-8 + 6 - 16 +12 +4 - 16) – 2(12+ 6 – 6 – 16) + (-6 + 16 - - 12 – 4)=38.
в) Вычислим определитель  , получив предварительно нули в первой строке. Используем свойство определителей: определитель не изменится, если ко всем элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же произвольное число. Умножим третий столбец определителя на 3 и прибавим к первому (3C3+C1).Полученный столбец запишем вместо первого. Затем третий столбец умножим на (-2) и прибавим ко второму (-2C3+C2.), и полученный столбец запишем вместо второго. Тогда в первой строке все элементы, кроме одного, будут нулями. Разложим полученный таким образом определитель по элементам первой строки и вычислим его:
, получив предварительно нули в первой строке. Используем свойство определителей: определитель не изменится, если ко всем элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же произвольное число. Умножим третий столбец определителя на 3 и прибавим к первому (3C3+C1).Полученный столбец запишем вместо первого. Затем третий столбец умножим на (-2) и прибавим ко второму (-2C3+C2.), и полученный столбец запишем вместо второго. Тогда в первой строке все элементы, кроме одного, будут нулями. Разложим полученный таким образом определитель по элементам первой строки и вычислим его:
 =
=  =
= 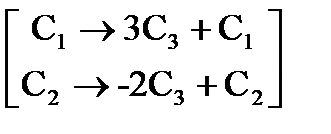 =
= 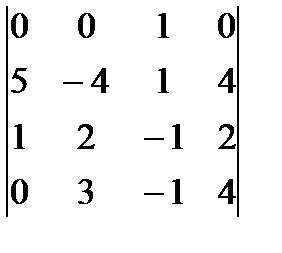 = 1*
= 1* 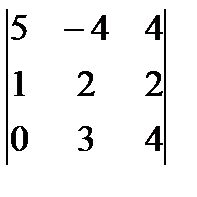 .= =
.= = 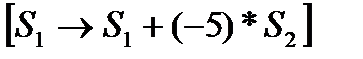 =
= 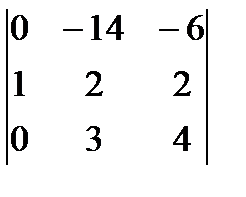 = -(-56+18)=38
= -(-56+18)=38
Пример 1.11.Не вычисляя определителя 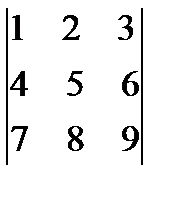 , показать, что он равен нулю.
, показать, что он равен нулю.
Решение. Вычтем из второй строки первую, получим определитель 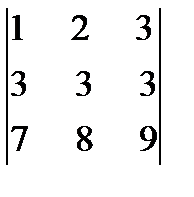 , равный исходному. Если из третьей строки также вычесть первую, то получится определитель
, равный исходному. Если из третьей строки также вычесть первую, то получится определитель 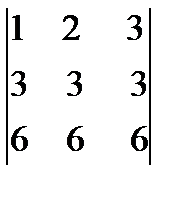 , в котором две строки пропорциональны. Такой определитель равен нулю.
, в котором две строки пропорциональны. Такой определитель равен нулю.
Пример 1.12.Вычислить определитель D = 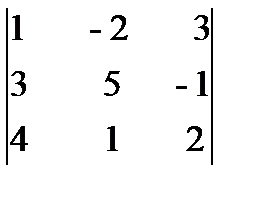 а) разложив его по элементам второго столбца, б) по правилу треугольников.
а) разложив его по элементам второго столбца, б) по правилу треугольников.
Дата добавления: 2015-09-29; просмотров: 1692;
