Решение. Произведение матрицы на матрицу (обозначается ) определено только в том случае, когда число столбцов матрицы равно числу строк матрицы
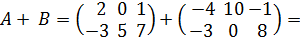
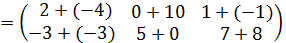 =
= 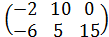 .
.
3) Умножение матриц.
Произведение матрицы 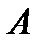 на матрицу
на матрицу 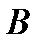 (обозначается
(обозначается 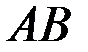 ) определено только в том случае, когда число столбцов матрицы
) определено только в том случае, когда число столбцов матрицы 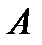 равно числу строк матрицы
равно числу строк матрицы 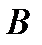 . В результате умножения получим матрицу
. В результате умножения получим матрицу 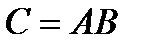 , у которой столько же строк, сколько их в матрице
, у которой столько же строк, сколько их в матрице 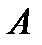 , и столько же столбцов, сколько их в матрице
, и столько же столбцов, сколько их в матрице 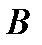 . Для удобства запоминания запишем это кратко:
. Для удобства запоминания запишем это кратко:
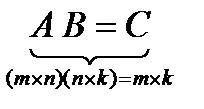
Если 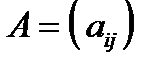 ,
, 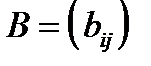 и
и 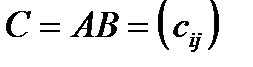 , то элементы
, то элементы 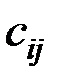 определяются следующим образом: каждый элемент
определяются следующим образом: каждый элемент 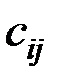 равен сумме произведений элементов i–ой строки матрицы
равен сумме произведений элементов i–ой строки матрицы 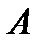 на соответствующие элементы j–ого столбца матрицы
на соответствующие элементы j–ого столбца матрицы 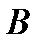 :
:
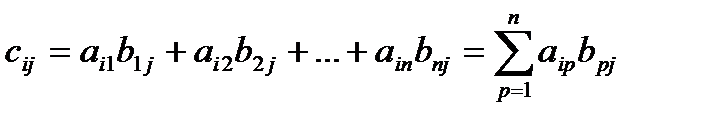 ,
,
где 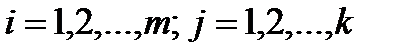 .
.
В качестве примера применения указанного правила приведем формулу перемножения квадратных матриц 2-го порядка:
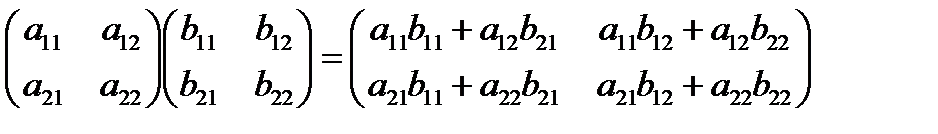 .
.
Дата добавления: 2015-09-29; просмотров: 526;
