Определители. Перестановкойчисел 1, 2,, n называется любое расположение этих чисел в определенном порядке

Перестановкойчисел 1, 2,..., n называется любое расположение этих чисел в определенном порядке. Число всех перестановок, которые можно образовать из n чисел, равно 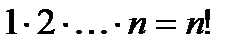. Например, из трех чисел 1, 2, 3 можно образовать 3!=6 перестановок: 123, 132, 312, 321, 231, 213. Говорят, что в данной перестановке числа i и j составляют инверсию(беспорядок), если i>j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего.

Обозначим общее число инверсий в перестановке 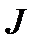символом 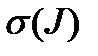. Перестановка 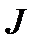называется четной, если число 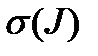– четное, и нечетной, если число 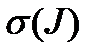– нечетное.

Так, в рассмотренном выше примере перестановка содержит 3 инверсии и, следовательно, является нечетной. Заметим, что перестановка 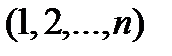не содержит ни одной инверсии, иначе говоря, содержит 0 инверсий. Следовательно, эта перестановка является четной.

Пример 1.9. Найти число инверсий в перестановке (2, 1, 3, 5, 4).

Решение.Для каждого члена в перестановке надо найти число элементов, меньших его и стоящих правее: для 2 – это 1 (только число 1 меньше 2, а остальные - 3, 4, 5 - не образуют инверсий), для 1 - 0 (все числа, стоящие правее, больше 1), для 3 – 0 (все числа, стоящие правее, больше 3), для 5 - 1 (число 4), для 4 - 0. Складывая все полученные числа 1+0+0+1+0=2. Получаем, что число инверсий в перестановке (2, 1, 3, 5, 4) равно 2: σ(J)=2.

Определителем квадратной матрицы A=( 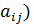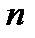-го порядка называется число, равное

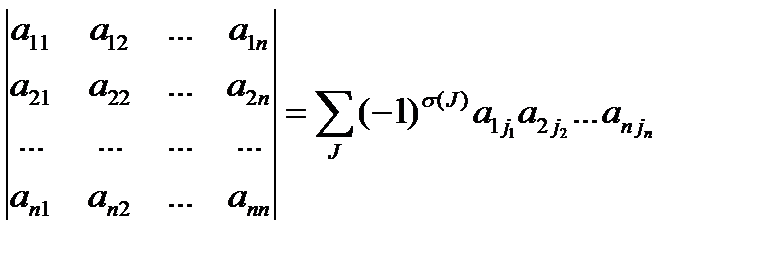, (2.2)

где суммирование распространяется на все перестановки 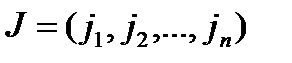, которые можно составить из чисел 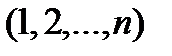. Количество слагаемых в правой части равенства (2.2) равно 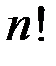, так как количество всех перестановок множества из 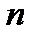элементов равно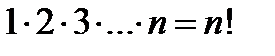

Определитель матрицы A=( 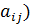обозначается Δ, или 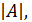или det(A).

Правила вычисления определителей 2-го и 3-го порядков легко выписать:

,

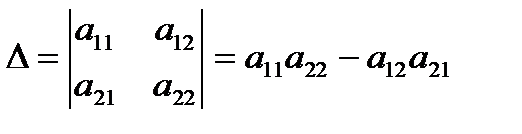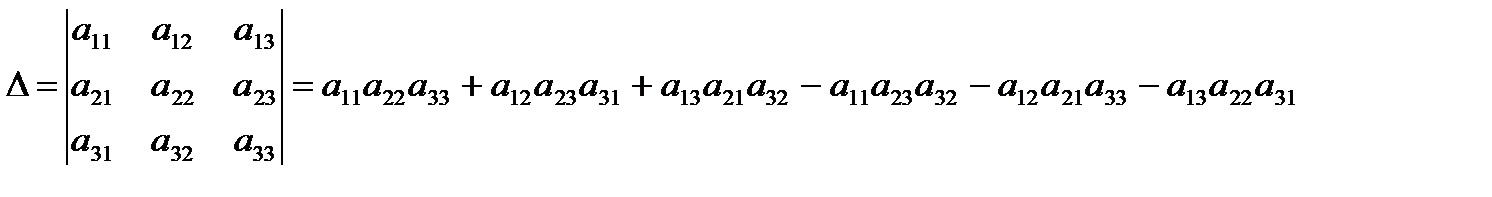
Приведенное правило вычисления определителей 3-го порядка называется правилом треугольников.