Определители матриц

Для каждой квадратной матрицы А вводится число |А|, которое называют ее определителем. Иногда его еще обозначают буквой D.

Это понятие является важным для решения ряда практических задач. Определим его через способ вычисления.

Для матрицы А первого порядка ее определителем называют ее единственный элемент |А| = D₁ = а₁₁.

Для матрицы А второго порядка ее определителем называют число, которое вычисляют по формуле |А| = D₂ = а₁₁* а₂₂ – а₂₁* а₁₂

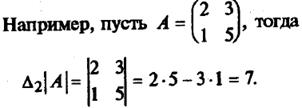
Для матрицы А третьего порядка ее определителем называют число, которое вычисляют по формуле

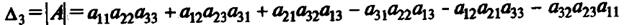
Оно представляет алгебраическую сумму, состоящую из 6 слагаемых, в каждое из которых входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Для запоминания формулы определителя принято пользоваться так называемым правилом треугольников или правилом Сарруса (рисунок 6.1).

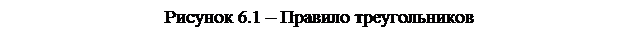На рисунке 6.1 схема слева показывает, каким образом выбирать элементы для слагаемых со знаком «плюс», - они находятся на главной диагонали и в вершинах равнобедренных треугольников, основания которых ей параллельны. Схема слева используется для слагаемых со знаком «минус»; на ней вместо главной диагонали берется так называемая побочная.

Определители более высоких порядков вычисляют рекуррентным способом, т.е. определитель четвертого порядка через определитель третьего порядка, определитель пятого порядка через определитель четвертого порядка и т.д. Для описания этого способа необходимо ввести понятия минора и алгебраического дополнения элемента матрицы (сразу же отметим, что сам способ, который будет рассмотрен далее, подходит и для определителей третьего и второго порядка).

МиноромМ_ij элемента а_ij матрицы n-го порядка называют определитель матрицы (n-1)-го порядка, полученной из матрицы А вычеркиванием i-й строки и j-го столбца.

Каждая матрица n-го порядка имеет n² миноров (n-1)-го порядка.

Алгебраическим дополнением A_ij элемента а_ij матрицы n-го порядка называют его минор, взятый со знаком (-1)^(i+j):

A_ij = (-1)^(i+j)*М_ij

Из определения следует, что A_ij = М_ij, если сумма номеров строки и столбца четная, и A_ij = -М_ij, если она нечетная.

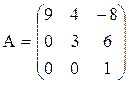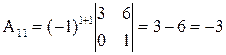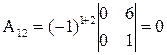Например, если , то _; и т.д.

Способ вычисления определителя состоит в следующем: определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

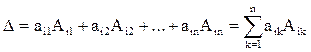(разложение по элементам i-й строки; );

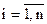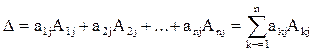(разложение по элементам j-го столбца; ).

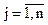Например,

Отметим, что и в общем случае определитель треугольной матрицы равен произведению элементов главной диагонали.

Сформулируем основные свойства определителей.

1. Если какая-либо строка или столбец матрицы состоит из одних нулей, то определитель равен 0 (следует из способа расчета).

2. Если все элементы какой-либо строки (столбца) матрицы умножить на одно и то же число, то и ее определитель умножится на это число (также следует из способа расчета – на расчет алгебраических дополнений общий множитель не влияет, а все остальные слагаемые умножены именно на это число).

Замечание: за знак определителя можно выносить общий множитель именно строки или столбца (в отличие от матрицы, за знак которой можно выносить общий множитель всех ее элементов). Например, 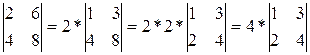, но .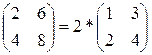

3. При транспонировании матрицы ее определитель не изменяется: |А^Т| = |А| (доказательство проводить не будем).

4. При перестановке местами двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

Для доказательства этого свойства вначале предположим, что переставлены две соседние строки матрицы: i-я и (i+1)-я. Для расчета определителя исходной матрицы осуществим разложение по i-й строке, а для определителя новой матрицы (с переставленными строками) – по (i+1)–й (которая в ней такая же, т.е. поэлементно совпадает). Тогда при расчете второго определителя каждое алгебраическое дополнение будет иметь противоположный знак, так как (-1) будет возводиться не в степень (i + j), а в степень (i + 1+ j), а в остальном формулы отличаться не будут. Таким образом, знак определителя изменится на противоположный.

Теперь предположим, что переставлены не соседние, а две произвольные строки, например, i-я и (i+t)-я. Такую перестановку можно представить как последовательное смещение i-й строки на t строк вниз, а (i+t)-й строки - на (t-1) строк вверх[1]. При этом знак определителя поменяется (t + t – 1) = 2t – 1 число раз, т.е. нечетное число раз. Следовательно, в конечном итоге он поменяется на противоположный.

Аналогичные рассуждения можно поменять для столбцов.

5. Если матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.

В самом деле, если одинаковые строки (столбцы) переставить местами, то будет получена та же самая матрица с тем же самым определителей. С другой стороны, по предыдущему свойству он должен поменять знак, т.е. D = -D Û D = 0.

6. Если элементы двух строк (столбцов) матрицы пропорциональны, то определитель равен 0.

Это свойство основано на предыдущем свойстве и выносе за скобку общего множителя (после выноса за скобку коэффициента пропорциональности в матрице будут одинаковые строки или столбцы, и в результате этот коэффициент будет умножаться на ноль).

7. Сумма произведений элементов любой строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) той же матрицы всегда равна 0: 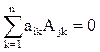при i ¹ j.

Чтобы доказать это свойство, достаточно заменить в матрице А j–ю строку на i–ю. В полученной матрице будет две одинаковые строки, поэтому ее определитель равен 0. С другой стороны, его можно вычислить разложением по элементам j -й строки: .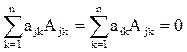

8. Определитель матрицы не изменяется, если к элементам строки или столбца матрицы прибавить элементы другой строки (столбца), умноженные на одно и тоже число.

В самом деле, пусть к элементам i–й строки прибавляют элементы j-й строки, умноженные на l. Тогда элементы новой i–й строки примут вид
(a_ik + la_jk, "k). Вычислим определитель новой матрицы разложением по элементам i-й строке (отметим, что алгебраические дополнения ее элементов при этом не изменятся):

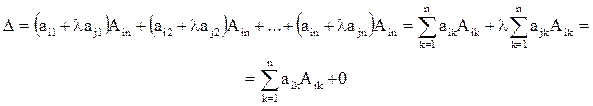Мы получили, что этот определитель не отличается от определителя исходной матрицы.

9. Определитель произведения матриц равен произведению их определителей: |АВ| = |А| * |В| (доказательство проводить не будем).

Рассмотренные выше свойства определителей используют для упрощения их вычисления. Обычно стараются преобразовать матрицу к такому виду, чтобы какой-либо столбец или строка содержали как можно больше нулей. После этого определитель легко найти разложением по этой строке или столбцу.