Матрицы. Матрица размера m х n – это прямоугольная таблица чисел, содержащая m строк и n столбцов

Линейная алгебра

Матрица размера m х n – это прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Матрицы принято обозначать заглавными латинскими буквами, а элементы – теми же, но строчными буквами с двойной индексацией.

Например, рассмотрим матрицу А размерности 2 х 3:

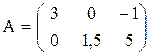
В этой матрице две строки (m = 2) и три столбца (n = 3), т.е. она состоит из шести элементов a_ij, где i - номер строки, j - номер столбца. При этом принимает значения от 1 до 2, а от одного до трех (записывается 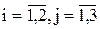). А именно, a₁₁= 3; a₁₂= 0; a₁₃= -1; a₂₁= 0; a₂₂= 1,5; a₂₃= 5.

Матрицы А и В одного размера (m х n ) называют равными, если они поэлементно совпадают, т.е. a_ij = b_ij для 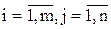, т.е. для любых i и j (можно записать "i, j).

Матрица-строка – это матрица, состоящая из одной строки, а матрица-столбец – это матрица, состоящая из одного столбца.

Например, 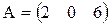- матрица-строка, а .

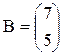Квадратная матрица n-го порядка – это матрица, в число строк равно числу столбцов и равно n.

Например, 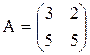- квадратная матрица второго порядка.

Диагональные элементы матрицы – это элементы, у которых номер строки равен номеру столбца (a_ij, i = j). Эти элементы образуют главную диагональ матрицы. В предыдущем примере главную диагональ образуют элементы a₁₁= 3 и a₂₂= 5.

Диагональная матрица – это квадратная матрица, в которой все недиагональные элементы равны нулю. Например, 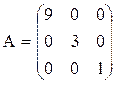- диагональная матрица третьего порядка. Если при этом все диагональные элементы равны единице, то матрица называется единичной (обычно обозначаются буквой Е). Например, 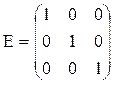- единичная матрица третьего порядка.

Матрица называется нулевой, если все ее элементы равны нулю.

Квадратная матрица называется треугольной, если все ее элементы ниже (или выше) главной диагонали равны нулю. Например, 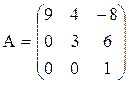- треугольная матрица третьего порядка.