Обратная матрица
Матрицу А-1 называют обратной по отношению к квадратной матрице А, если при умножении этой матрицы на матрицу А как справа, так и слева получается единичная матрица: А-1 * А = А * А-1 = Е.
Из определения следует, что обратная матрица является квадратной матрицей того же порядка, что и матрица А.
Можно отметить, что понятие обратной матрицы аналогично понятию обратного числа (это число, которое при умножении на данное число дает единицу: а*а-1= а*(1/а) = 1).
Все числа, кроме нуля, имеют обратные числа.
Чтобы решить вопрос о том, имеет ли квадратная матрица обратную, необходимо найти ее определитель. Если определитель матрицы равен нулю, то такая матрица называется вырожденной, или особенной.
Необходимое и достаточное условие существования обратной матрицы: обратная матрица существует и единственна тогда и только тогда, когда исходная матрица невырожденная.
Докажем необходимость. Пусть матрица А имеет обратную матрицу А-1, т.е. А-1 * А = Е. Тогда |А-1 * А| = |А-1| * |А| = |Е| = 1. Следовательно,
|А| ¹ 0.
Докажем достаточность. Чтобы его доказать, необходимо просто описать способ вычисления обратной матрицы, который мы всегда сможем применить для невырожденной матрицы.
Итак, пусть |А| ¹ 0. Транспонируем матрицу А. Для каждого элемента АТ найдем алгебраическое дополнение и составим из них матрицу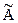 
, которую называют присоединенной(взаимной, союзной): 
.
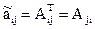Найдем произведение присоединенной матрицы и исходной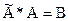 
. Получим 
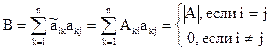. Таким образом матрица В – диагональная. На ее главной диагонали стоят определители исходной матрицы, а все остальные элементы – нули:
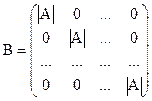
Аналогично можно показать, что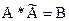 
.
Если разделить все элементы матрицы на |А|, то будет получена единичная матрица Е.
Таким образом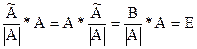 
, т.е. 
.
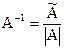Докажем единственность обратной матрицы. Предположим, что существует другая обратная матрица для А, отличная от А-1. Обозначим ее X. Тогда А * Х = Е. Умножим слева обе части равенства на А-1.
А-1 * А * Х = А-1 * Е
Е * Х = А-1
Х = А-1
Единственность доказана.
Итак, алгоритм вычисления обратной матрицы состоит из следующих шагов:
1. Найти определитель матрицы |А| . Если |А| = 0, то матрица А - вырожденная, и обратную матрицу найти нельзя. Если |А| ¹ 0, то переходят к следующему шагу.
2. Построить транспонированную матрицу АТ.
3. Найти алгебраические дополнения элементов транспонированной матрицы и построить присоединенную матрицу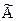 
.
4. Вычислить обратную матрицу, разделив присоединенную матрицу на |А|.
5. Можно проверить правильность вычисления обратной матрицы в соответствии с определением: А-1 * А = А * А-1 = Е.
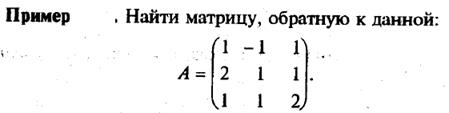
1. Найдем определитель этой матрицы по правилу треугольников:
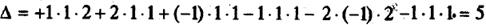¹ 0.
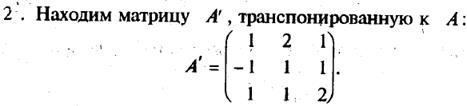
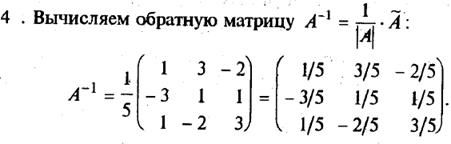
Проверку опустим.
Можно доказать следующие свойства обращения матриц:
1) |А-1| = 1/|А|
2) (А-1)-1 = А
3) (Аm)-1 = (А-1)m
4) (АB)-1 = B-1 * А-1
5) (А-1)T = (АT)-1
Дата добавления: 2015-10-06; просмотров: 785;