Ранг матрицы. Минором k-го порядка матрицы А размера m х n называют определитель квадратной матрицы k-го порядка, которая получена из матрицы А вычеркиванием каких-либо

Минором k-го порядка матрицы А размера m х n называют определитель квадратной матрицы k-го порядка, которая получена из матрицы А вычеркиванием каких-либо строк и столбцов.

Из определения следует, что порядок минора не превосходит меньшего из ее размеров, т.е. k £ min {m; n}. Например, из матрицы А_5х3 можно получить квадратные подматрицы первого, второго и третьего порядков (соответственно, рассчитать миноры этих порядков).

Рангом матрицы называют наивысший порядок отличных от нуля миноров этой матрицы (обозначают rang А, или r(А)).

Из определения следует, что

1) ранг матрицы не превосходит меньшего из ее размеров, т.е.
r(А) £ min {m; n};

2) r(А) = 0 тогда и только тогда, когда матрица нулевая (все элементы матрицы равны нулю), т.е. r(А) = 0 Û А = 0;

3) для квадратной матрицы n-го порядка r(А) = n тогда и только тогда, когда эта матрица А невырожденная, т.е. r(А) = n Û |А| ¹ 0.

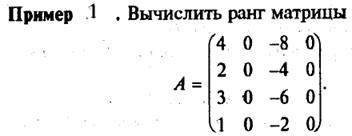
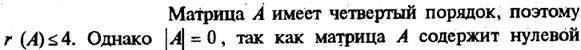
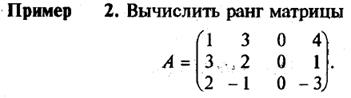
На самом деле, для этого достаточно вычислить только один такой минор (тот, который получен вычеркиванием третьего столбца (потому что в остальных будет присутствовать нулевой третий столбец, и поэтому они равны нулю).

По правилу треугольника 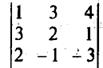= 1*2*(-3) + 3*1*2 + 3*(-1)*4 – 4*2*2 – 1*(-1)*1 – 3*3*(-3) = -6 +6 – 12 – 16 + 1 +27 = 0.

Поскольку все миноры третьего порядка нулевые, r(А) £ 2. Так как существует ненулевой минор второго порядка, например,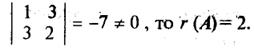

Очевидно, что использованные нами приемы (рассмотрение всевозможных миноров) не подходят для определения ранга в более сложных случаях ввиду большой трудоемкости. Обычно для нахождения ранга матрицы используют некоторые преобразования, которые называют элементарными:

1). Отбрасывание нулевых строк (столбцов).

2). Умножение всех элементов строки или столбца матрицы на число, отличное от нуля.

3). Изменение порядка строк (столбцов) матрицы.

4). Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

5). Транспонирование.

Если матрица А получена из матрицы B элементарными преобразованиями, то эти матрицы называют эквивалентными и обозначают А ~ В.

Теорема. Элементарные преобразования матрицы не изменяют ее ранг.

Доказательство теоремы следует из свойств определителя матрицы. В самом деле, при этих преобразованиях определители квадратных матриц либо сохраняются, либо умножаются на число, не равное нулю. В результате наивысший порядок отличных от нуля миноров исходной матрицы остается прежним, т.е. ее ранг не меняются.

С помощью элементарных преобразований матрицу приводят к так называемому ступенчатому виду (преобразуют в ступенчатую матрицу), т.е. добиваются, чтобы в эквивалентной матрице под главной диагональю стояли только нулевые элементы, а на главной диагонали – ненулевые:

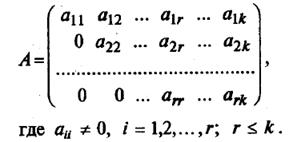
Ранг ступенчатой матрицы равен r, так как вычеркиванием из нее столбцов, начиная с (r + 1)-го и дальше можно получить треугольную матрицу r-го порядка, определитель которой будет отличен от нуля, так как будет представлять собой произведение ненулевых элементов (следовательно, имеется минор r-го порядка, не равный нулю):

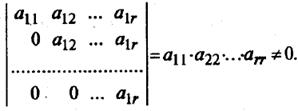
Пример. Найти ранг матрицы

1). Если а₁₁ = 0 (как в нашем случае), то перестановкой строк или столбцов добьемся того, чтобы а₁₁ ¹ 0. Здесь поменяем местами 1-ю и 2-ю строки матрицы:

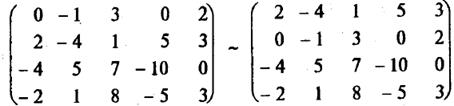
2). Теперь а₁₁ ¹ 0. Элементарными преобразованиями добьемся того, чтобы все остальные элементы в первом столбце равнялись нулю. Во второй строке a₂₁ = 0. В третьей строке a₃₁ = -4. Чтобы вместо (-4) стоял 0, прибавим к третьей строке первую строку, умноженную на 2 (т.е. на (-а₃₁/а₁₁) = -(-4)/2 =
= 2). Аналогично к четвертой строке прибавим первую строку (умноженную на единицу, т.е. на (-а₄₁/а₁₁) = -(-2)/2 = 1).

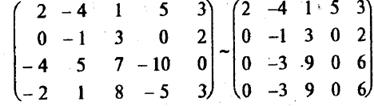
3). В полученной матрице а₂₂ ¹ 0 (если бы было а₂₂ = 0, то можно было бы снова переставить строки). Добьемся, чтобы ниже диагонали во втором столбце тоже стояли нули. Для этого к 3-й и 4-й строкам прибавим вторую строку, умноженную на -3 ((-а₃₂/а₂₂) = (-а₄₂/а₂₂) = -(-3)/(-1) = -3):

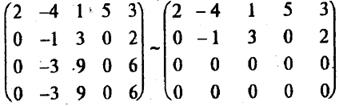
4). В полученной матрице две последние строки – нулевые, и их можно отбросить:

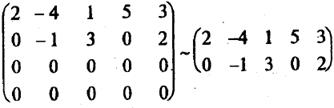
Получена ступенчатая матрица, состоящая из двух строк. Следовательно, r(A) = 2.