Метод решения систем линейных уравнений с квадратной матрицей по формулам Крамера

Пусть n = 2:

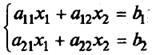
Если обе части первого уравнения умножить на a₂₂, а обе части второго – на (-a₁₂), и затем сложить полученные уравнения, то мы исключим из системы переменную x₂. Аналогично можно исключить переменную x₁ (умножив обе части первого уравнения на (-a₂₁), а обе части второго – на a₁₁). В результате получим систему:

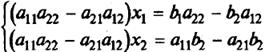
Выражение в скобках есть определитель системы

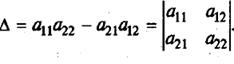
Обозначим

Тогда система примет вид:

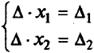
Из полученной системы следует, что если определитель системы
D ¹ 0, то система будет совместной и определенной. Ее единственное решение можно вычислить по формулам:

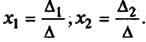
Если D = 0, а D₁ ¹ 0 и/или D₂ ¹ 0, то уравнения системы примут вид 0*х₁ = D₂ и/или0*х₁ = D₂. В этом случае система будет несовместной.

В случае, когда D = D₁ = D₂ = 0, система будет совместной и неопределенной (будет иметь бесконечное множество решений), так как примет вид:

Теорема Крамера (доказательство опустим). Если определитель матрицы системы n уравнений D не равен нулю, то система имеет единственное решение, определяемое по формулам:

,

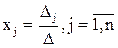где D_j - определитель матрицы, получаемой из матрицы А заменой j-го столбца столбцом свободных членов.

Вышеприведенные формулы называют формулами Крамера.

В качестве примера решим этим методом систему, которую до этого решали методом обратной матрицы:

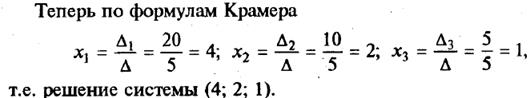
Недостатки рассмотренных методов:

1) существенная трудоемкость (вычисление определителей и нахождение обратной матрицы);

2) ограниченная область применения (для систем с квадратной матрицей).

Реальных экономические ситуации чаще моделируются системами, в которых число уравнений и переменных довольно значительное, причем уравнений больше, чем переменных Поэтому на практике более распространен следующий метод.

Метод Гаусса (метод последовательного исключения переменных)

Этот метод используется для решения системы m линейных уравнений с n переменными в общем виде. Его суть заключается в применении к расширенной матрице системы равносильных преобразований, с помощью которых система уравнений преобразуется к виду, когда ее решения становится легко найти (если они есть).

Это такой вид, в котором левая верхняя часть матрицы системы будет представлять собой ступенчатую матрицу. Этого добиваются с помощью тех же приемов, с помощью которых получали ступенчатую матрицу с целью определения ранга. При этом применяют к расширенной матрице элементарные преобразования, которые позволят получить равносильную систему уравнений. После этого расширенная матрица примет вид:

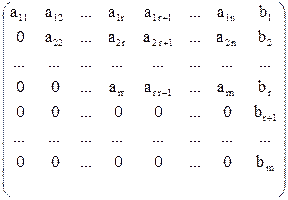
Получение такой матрицы называют прямым ходом метода Гаусса.

Нахождение из соответствующей системы уравнений значений переменных называют обратным ходом метода Гаусса. Рассмотрим его.

Отметим, что последние (m – r) уравнений примут вид:

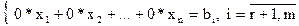
Если хотя бы одно из чисел 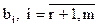не равно нулю, то соответствующее равенство будет ложным, а вся система несовместной.

Поэтому для любой совместной системы 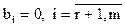. В этом случае последние (m – r) уравнений при любых значениях переменных будут тождествами 0 = 0, и их можно не принимать во внимание при решении системы (просто отбросить соответствующие строки).

После этого система примет вид:

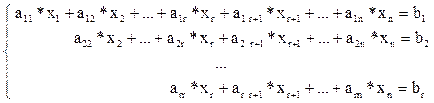
Рассмотрим вначале случай, когда r = n. Тогда система примет вид:

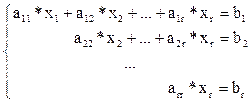
Из последнего уравнения системы можно однозначно найти x_r.

Предпоследнее уравнение будет иметь вид:

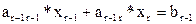
Зная x_r, из него можно однозначно выразить x_r-1. Затем из предыдущего уравнения, зная x_r и x_r-1, можно выразить x_r-2 и т.д. до x₁.

Итак, в этом случае система будет совместной и определенной.

Например, решим систему уравнений:

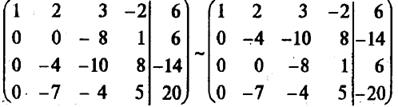
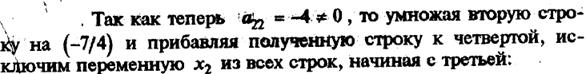
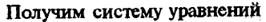
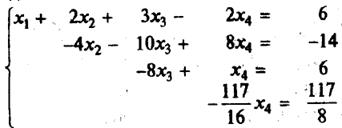
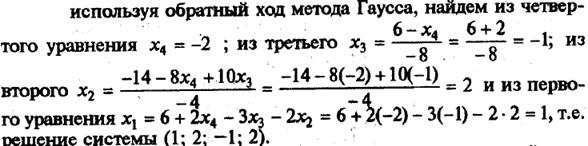
Теперь рассмотрим случай, когда r < n. Первые r переменных будем называть базисными (основными), а все остальные – небазисными (неосновными, свободными). Последнее уравнение системы будет иметь вид:

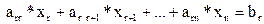
Из этого уравнения можно выразить базисную переменную x_r через небазисные:

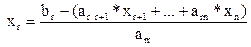
Предпоследнее уравнение будет иметь вид:

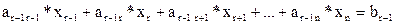
Подставив в него вместо x_r полученное выражение, можно будет выразить базисную переменную x_r-1 через небазисные. И т.д. до переменной x₁. Чтобы получить решение системы, можно приравнять небазисные переменные к произвольным значениям и после этого вычислить базисные переменные по полученным формулам. Таким образом, в этом случае система будет совместной и неопределенной (иметь бесконечное множество решений).

Например, решим систему уравнений:

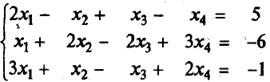
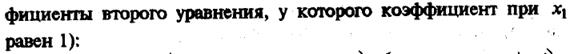
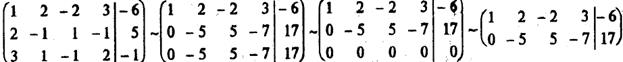
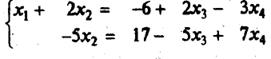
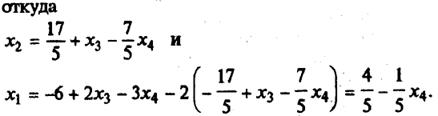
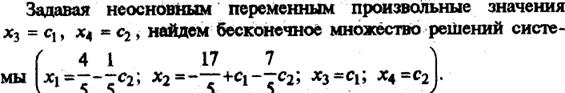
Совокупность базисных переменных будем называть базисом системы. Совокупность столбцов коэффициентов при них тоже будем называть базисом (базисными столбцами), или базисным минором матрицы системы. То решение системы, в котором все небазисные переменные равны нулю, будем называть базисным решением.

В предыдущем примере базисным решением будет (4/5; -17/5; 0; 0) (переменные х₃ и х₄ (с₁ и с₂) приравнены к нулю, а базисные переменные х₁ и х₂ рассчитаны через них). Чтобы привести пример небазисного решения, надо приравнять х₃ и х₄ (с₁ и с₂) к произвольным числам, неравным одновременно нулю, и рассчитать через них остальные переменные. Например, при с₁ = 1 и с₂ = 0 получим небазисное решение – (4/5; -12/5; 1; 0). Подстановкой легко убедиться, что оба решения – верные.

Очевидно, что в неопределенной системе небазисных решений может быть бесконечно много. Сколько может быть базисных решений? Каждой строке преобразованной матрицы должна соответствовать одна базисная переменная. Всего в задаче n переменных, а базисных строк – r. Поэтому число всевозможных наборов базисных переменных не может превысить число сочетаний из n по r[2]. Оно может быть меньше, чем 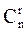, потому что не всегда можно преобразовать систему к такому виду, чтобы именно этот набор переменных был базисным.

Что это за вид? Это такой вид, когда матрица, образованная из столбцов коэффициентов при этих переменных, будет ступенчатой, и при этом будет состоять из r строк. Т.е. ранг матрицы коэффициентов при этих переменных должен быть равен r. Больше r он быть не может, так как число столбцов равно r. Если он окажется меньше r, то это говорит о линейной зависимости столбцов при переменных. Такие столбцы не могут составить базис.

Рассмотрим, какие еще базисные решения могут быть найдены в рассмотренном выше примере. Для этого рассмотрим всевозможные сочетания из четырех переменных по две базисных. Таких сочетаний будет 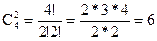, причем одно из них (х₁ и х₂) уже было рассмотрено.

Возьмем переменные х₁ и х₃. Найдем ранг матрицы коэффициентов при них:

Так как он равен двум, они могут быть базисными. Приравняем небазисные переменные х₂ и х₄ к нулю: х₂ = х₄ = 0. Тогда из формулы
х₁ = 4/5 – (1/5)*х₄ следует, что х₁ = 4/5, а из формулы х₂ = -17/5 + х₃ -
- (7/5)*х₄ = -17/5 + х₃ следует, что х₃ = х₂ +17/5 = 17/5. Таким образом, мы получим базисное решение (4/5; 0; 17/5; 0).

Аналогично можно получить базисные решения для базисных переменных х₁ и х₄ – (9/7; 0; 0; -17/7); х₂ и х₄ – (0; -9; 0; 4); х₃ и х₄ – (0; 0; 9; 4).

Переменные х₂ и х₃ в этом примере нельзя взять в качестве базисных, так как ранг соответствующей матрицы равен единице, т.е. меньше двух:

.

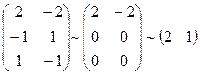Возможен и другой подход к определению того, можно или нет составить базис из некоторых переменных. При решении примера в итоге преобразования матрицы системы к ступенчатому виду она приняла вид:

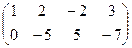
Выбирая пары переменных, можно было рассчитать соответствующие миноры этой матрицы. Легко убедиться, что для всех пар, кроме х₂ и х₃, они не равны нулю, т.е. столбцы линейно независимы. И только для столбцов при переменных х₂ и х₃ 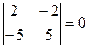, что говорит об их линейной зависимости.

Рассмотрим еще один пример. Решим систему уравнений

Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво - оно привелось к неверному равенству 0 = -1, следовательно, данная система несовместна.

Метод Жордана-Гаусса[3] представляет собой развитие метода Гаусса. Суть его состоит в том, что расширенную матрицу системы преобразуют к виду, когда коэффициенты при r переменных образуют единичную матрицу с точностью до перестановки строк или столбцов[4] (где r – ранг матрицы системы).

Решим этим методом систему:

Рассмотрим расширенную матрицу системы:

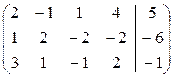
В этой матрице выберем единичный элемент. Например, коэффициент при х₂ в третьем ограничении[5]. Добьемся, чтобы в остальных строках в этом столбце стояли нули, т.е. сделаем столбец единичным. В процессе преобразований будем называть этот столбец разрешающим (ведущим, ключевым). Третье ограничение (третью строку) тоже будем называть разрешающей. Сам элемент, который стоит на пересечении разрешающих строки и столбца (здесь это единица), тоже называют разрешающим.

В первой строке сейчас стоит коэффициент (-1). Чтобы получить на его месте ноль, умножим третью строку на (-1) и вычтем результат из первой строки (т.е. просто сложим первую строку с третьей).

Во второй строке стоит коэффициент 2. Чтобы получить на его месте ноль, умножим третью строку на 2 и вычтем результат из первой строки.

Результат преобразований будет иметь вид:

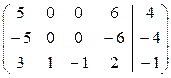
Из этой матрицы хорошо видно, что одно из первых двух ограничений можно вычеркнуть (соответствующие строки пропорциональны, т.е. эти уравнения следуют друг из друга). Вычеркнем, например, второе:

Итак, в новой системе два уравнения. Получен единичный столбец (второй), причем единица здесь стоит во второй строке. Запомним, что второму уравнению новой системы у нас будет соответствовать базисная переменная х₂.

Выберем базисную переменную для первой строки. Это может быть любая переменная, кроме х₃ (потому что при х₃ в первом ограничении стоит нулевой коэффициент, т.е. набор переменных х₂ и х₃ здесь базисным быть не может). Можно взять первую или четвертую переменную.

Выберем х₁. Тогда разрешающим элементом будет 5, и обе части разрешающего уравнения придется разделить на пять, чтобы получить в первом столбце первой строки единицу.

Добьемся, чтобы в остальных строках (т.е. во второй строке) в первом столбце стояли нули. Так как сейчас во второй строке стоит не ноль, а 3, надо вычесть из второй строки элементы преобразованной первой строки, умноженные на 3:

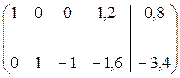
Из полученной матрицы можно непосредственно извлечь одно базисное решение, приравняв небазисные переменные к нулю, а базисные – к свободным членам в соответствующих уравнениях: (0,8; -3,4; 0; 0). Можно также вывести общие формулы, выражающие базисные переменные через небазисные: х₁ = 0,8 – 1,2х₄; х₂ = -3,4 + х₃ + 1,6х₄. Эти формулы описывают все бесконечное множество решений системы (приравнивая х₃ и х₄ к произвольным числам, можно вычислить х₁ и х₂).

Отметим, что суть преобразований на каждом этапе метода Жордана-Гаусса заключалась в следующем:

1) разрешающую строку делили на разрешающий элемент, чтобы получить на его месте единицу,

2) из всех остальных строк вычитали преобразованную разрешающую, умноженную на тот элемент, который стоял в данной строке в разрешающем столбце, чтобы получить на месте этого элемента ноль.

Рассмотрим еще раз преобразованную расширенную матрицу системы:

Из этой записи видно, что ранг матрицы системы А равен r.

В ходе проведенных рассуждений мы установили, что система будет совместной тогда и только тогда, когда 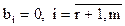. Это означает, что расширенная матрица системы будет иметь вид:

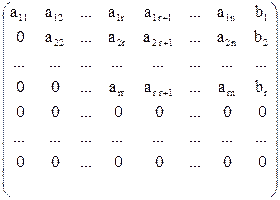
Отбрасывая нулевые строки, мы получим, что ранг расширенной матрицы системы тоже равен r.

Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.

Вспомним, что ранг матрицы равен максимальному числу ее линейно независимых строк. Из этого следует, что если ранг расширенной матрицы меньше числа уравнений, то уравнения системы линейно зависимы, и одно или несколько из них могут быть исключены из системы (поскольку являются линейной комбинацией остальных). Система уравнений будет линейно независимой лишь в том случае, если ранг расширенной матрицы равен числу уравнений.

При этом для совместных систем линейных уравнений можно утверждать, что если ранг матрицы равен числу переменных, то система имеет единственное решение, а если он меньше числа переменных, то система неопределенная и имеет бесконечно много решений.

[1] Например, пусть в матрице пять строк (исходный порядок строк – 12345). Надо поменять вторую строку и пятую. Чтобы вторая строка попала на место пятой, «сдвинулась» вниз, последовательно три раза поменяем соседние строки: вторую и третью (13245), вторую и четвертую (13425) и вторую и пятую (13452). Затем, чтобы пятая строка попала на место второй в исходной матрице, надо «сдвинуть» вверх пятую строку путем только двух последовательных перемен: пятой и четвертой строк (13542) и пятой и третьей (15342).

[2] Числом сочетаний из n по r 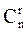называют число всех различных
r–элементных подмножеств n–элементного множества (различными множествами считаются те, которые имеют различный состав элементов, порядок отбора при этом не важен). Его вычисляют по формуле: 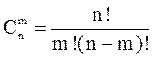. Напомним смысл знака “!” (факториал): 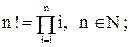0!=1.)

[3] Поскольку этот метод более распространен, чем рассмотренный ранее метод Гаусса, и по своей сути представляет собой сочетание прямого и обратного хода метода Гаусса, его тоже иногда называют методом Гаусса, опуская первую часть названия.

[4] Например, .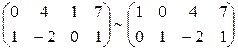

[5] Если бы в матрице системы не было единиц, то можно было бы, например, разделить обе части первого уравнения на два, и тогда первый коэффициент стал бы единичным; или т.п.