Ранг матрицы
Рассмотрим прямоугольную матрицу (2.1). Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядкаматрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим.
Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Любой минор порядка r называется базисным. Строки и столбцы, на пересечении которых стоит базисный минор, называются
базисными строками и базисными столбцами.
Сформулируем основную теорему о базисном миноре, но для этого нам потребуются следующие определения:
Вектор-столбец (строка) 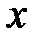 называется линейной комбинациейвектор-столбцов (строк)
называется линейной комбинациейвектор-столбцов (строк) 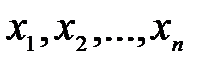 векторного пространства с коэффициентами
векторного пространства с коэффициентами 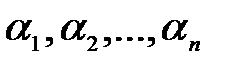 , если он равен сумме произведений этих векторов на эти коэффициенты:
, если он равен сумме произведений этих векторов на эти коэффициенты: 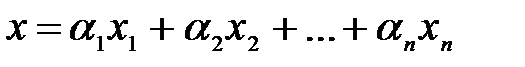 ;.
;.
Система 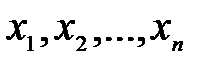 вектор-столбцов (строк) называется линейно зависимой, если найдутся такие числа
вектор-столбцов (строк) называется линейно зависимой, если найдутся такие числа 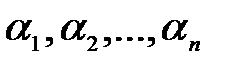 , из которых хотя бы одно отлично от нуля, что выполняется равенство
, из которых хотя бы одно отлично от нуля, что выполняется равенство 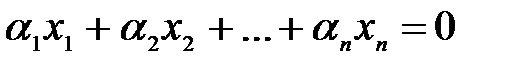 ; в противном случае данная система вектор-столбцов (строк) называется линейно независимой, то есть указанное равенство возможно лишь в случае, когда все
; в противном случае данная система вектор-столбцов (строк) называется линейно независимой, то есть указанное равенство возможно лишь в случае, когда все 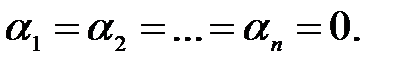
Теорема 1.3 (о базисном миноре).Базисные строки(столбцы) линейно независимы. Любая строка (столбец) матрицы А является линейной комбинацией базисных строк (столбцов)
Ранг матрицы А обозначается через r(A). Очевидно, что выполняется соотношение
0 £ r(A) £ min (m, n).
Ранг матрицы находится либо методом окаймления миноров (перебора миноров и выбора из них ненулевого минора наибольшего порядка), либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.
С помощью элементарных преобразований матрицу 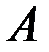 можно привести к виду
можно привести к виду
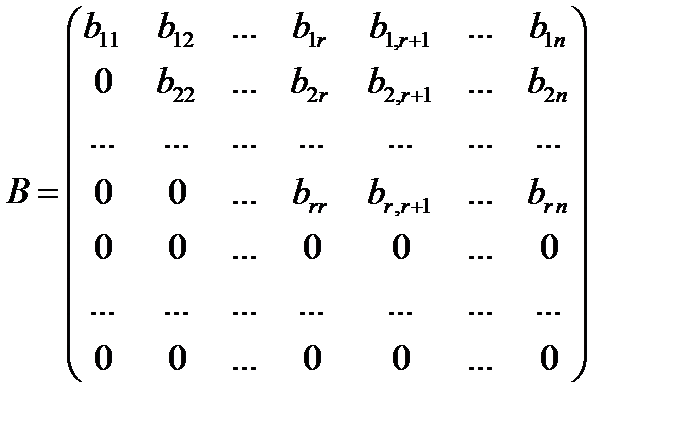 ,
,
в котором элементы 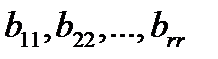 отличны от нуля, а элементы, расположенные ниже, равны нулю. Матрицу
отличны от нуля, а элементы, расположенные ниже, равны нулю. Матрицу 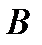 такого вида называют ступенчатой. После приведения матрицы
такого вида называют ступенчатой. После приведения матрицы 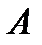 к ступенчатому виду можно сразу записать, что
к ступенчатому виду можно сразу записать, что 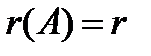 .
.
В самом деле, 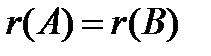 (т.к. элементарные преобразования не меняют ранга). Но у матрицы
(т.к. элементарные преобразования не меняют ранга). Но у матрицы 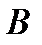 существует отличный от нуля минор порядка
существует отличный от нуля минор порядка 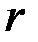 :
:
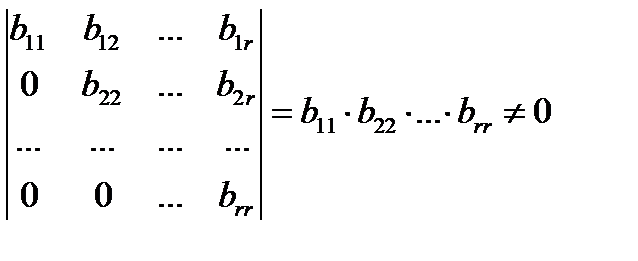 ,
,
а любой минор порядка 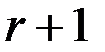 содержит нулевую строку и поэтому равен нулю.
содержит нулевую строку и поэтому равен нулю.
Сформулируем теперь практическое правило вычисления ранга матрицы 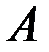 с помощью элементарных преобразований: для нахождения ранга матрицы
с помощью элементарных преобразований: для нахождения ранга матрицы 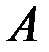 следует с помощью элементарных преобразований привести ее к ступенчатому виду
следует с помощью элементарных преобразований привести ее к ступенчатому виду 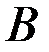 . Тогда ранг матрицы
. Тогда ранг матрицы 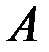 будет равен числу ненулевых строк в полученной матрице
будет равен числу ненулевых строк в полученной матрице 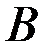 .
.
Пример 1.17. Найти методом окаймления миноров ранг матрицы 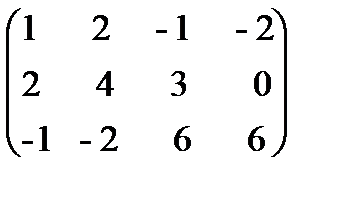 и написать один из базисных миноров.
и написать один из базисных миноров.
Решение.Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М1 = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор M2 = 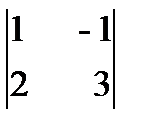 , отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего два (можно
, отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего два (можно
добавить второй столбец или четвертый). Вычисляем их: 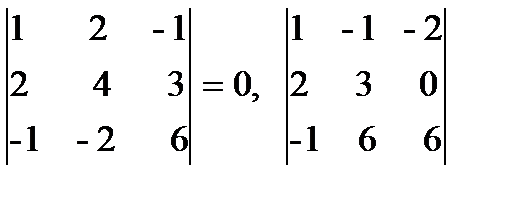 = 0. Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум, а базисным минором будет, например M2 =
= 0. Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум, а базисным минором будет, например M2 = 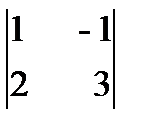 .
.
Пример 1.18. Найти ранг матрицы А= 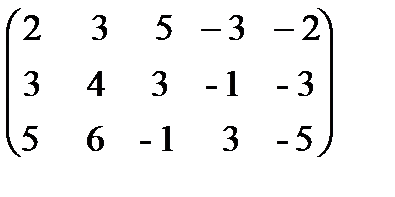 и привести ее к ступенчатому виду.
и привести ее к ступенчатому виду.
Решение.Из второй строки вычтем первую и переставим эти строки: 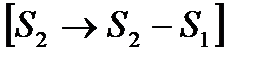 ~
~ 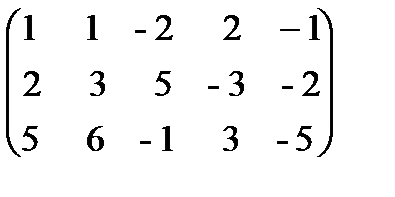 . Теперь из второй и третьей строк вычтем
. Теперь из второй и третьей строк вычтем  первую, умноженную соответственно на 2 и 5
первую, умноженную соответственно на 2 и 5 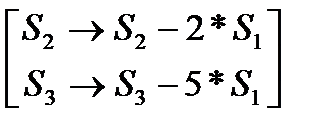 ~:
~: 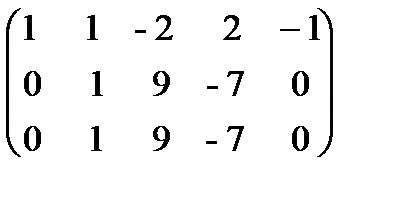 ; из третьей строки вычтем первую; получим матрицу В =
; из третьей строки вычтем первую; получим матрицу В = 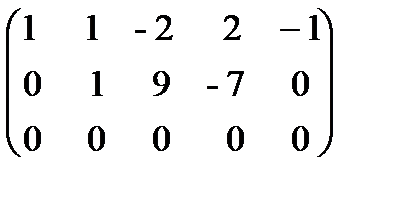 , которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Базисным минором является минор
, которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Базисным минором является минор 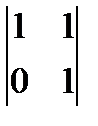 .
.
Дата добавления: 2015-09-29; просмотров: 696;
