Решение. а) Разложим определитель по элементам второго столбца:

а) Разложим определитель по элементам второго столбца:

D = a₁₂A₁₂ + a₂₂A₂₂+a₃₂A₃₂=

= .

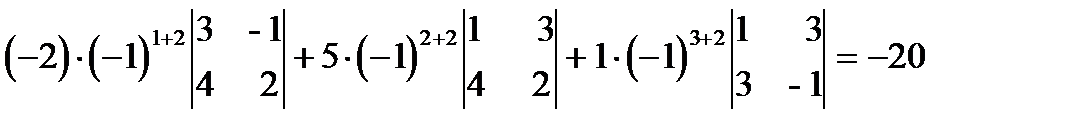б) По правилу треугольников:

D = 10+8+9-60+12+1 = -20.

Пример 1.13. Вычислить определитель

Δ = ,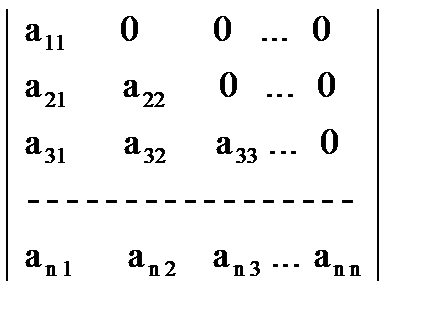

в котором все элементы по одну сторону от главной диагонали равны нулю.

Решение.Разложим определитель Δ по первой строке:

Δ = a₁₁ A₁₁ = .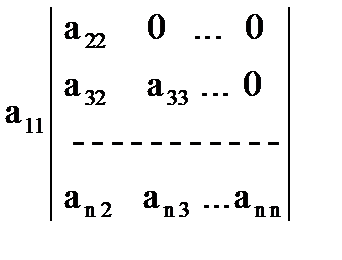

Определитель, стоящий справа, можно снова разложить по первой строке, тогда получим:

Δ = .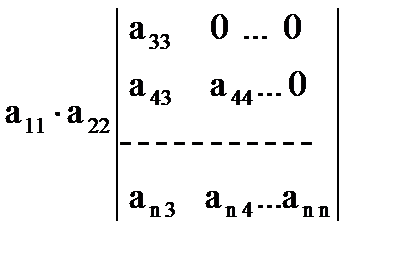

И так далее. После n шагов придем к равенству Δ = а₁₁ а_22... a_nn.

Пример 1.14. Вычислить определитель .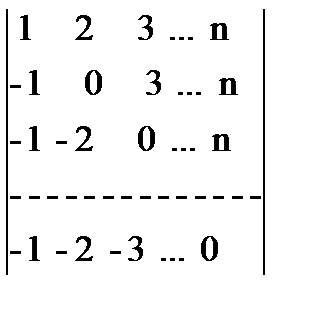

Решение.Если к каждой строке определителя, начиная со второй, прибавить первую строку, то получится определитель, в котором все элементы, находящиеся ниже главной диагонали, будут равны нулю. А именно, получим определитель: 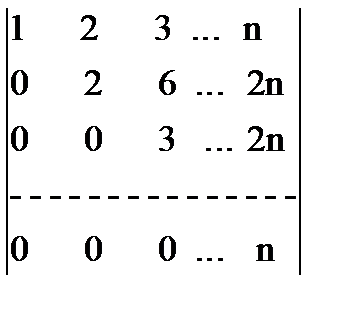, равный исходному.

Рассуждая, как в предыдущем примере найдем, что он равен произведению элементов главной диагонали, т.е. n!. Способ, с помощью которого вычислен данный определитель, называется способом приведения к треугольному виду.